练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,在直角坐标系中,直线y=6-x与双曲线y=(x>0)的图象相交于点A,B,设点A的坐标为(m,n),那么以m为长、n为宽的矩形的面积和周长分别为(　　)

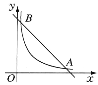
    A. 4,6 B. 4,12 C. 8,6 D. 8,12

    【答案】B

    【解析】

    此题首先要观察题目，求的是矩形的面积和周长，首先表示出矩形的面积：mn，正好符合反比例函数的特点，因此根据点A在反比例函数的图象上即可得解；然后求矩形的周长：2（x+y），此时发现周长的表达式正好符合直线AB的解析式，根据A点在直线AB的函数图象上即可得解．

    ∵点A（m，n）在y=6-x与双曲线y＝ (x＞0)的图象上，

    ∴n=6-m，n=，

    ∴m+n=6，mn=4；

    ∴矩形的面积为：mn=4，矩形的周长为：2（m+n）=12；

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为米，中午时不能挡光. 如图，某旧楼的一楼窗台高1米，要在此楼正南方米处再建一幢新楼. 已知该地区冬天中午时阳光从正南方照射，并且光线与水平线的夹角最小为°，在不违反规定的情况下，请问新建楼房最高_____________米. (结果精确到1米.,)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

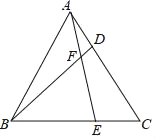
    【题目】如图，△ABC是等边三角形，D，E分别是AC，BC边上的点，且AD＝CE，连接BD，AE相交于点F．

    （1）∠BFE的度数是多少；

    （2）如果，那么等于多少；

    （3）如果时，请用含n的式子表示AF，BF的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】晚上,小亮走在大街上发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3m,左边的影子长为1.5m,又知自己身高1.80m,两盏路灯的高相同,两盏路灯之间的距离为12m,则路灯的高为(　　)

    A. 6.6m B. 6.7m C. 6.8m D. 6.9m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某空调厂的装配车间计划组装9000台空调.

    (1)从组装空调开始,每天组装的台数m(单位:台/天)与生产时间t(单位:天)之间有怎样的函数关系?

    (2)原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前10天上市,那么原装配车间每天至少要组装多少台空调?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

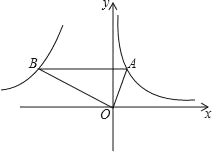
    【题目】如图，Rt△ABO中，∠AOB＝90°，点A在第一象限，点B在第二象限，且AO：BO＝1：2，若经过点A的反比例函数解析式为y＝，则经过点B（x，y）的反比例函数解析式为（　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

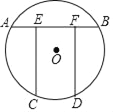
    【题目】如图，为一圆洞门．工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑，点A、B、C、D在⊙O上，CE⊥AB于E，DF⊥AB于F，且AB＝2，EF＝，＝120°．

    (1)求出圆洞门⊙O的半径；

    (2)求立柱CE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝﹣x2+bx+c（b，c均为常数）的图象经过两点A（2，0），B（0，﹣6）．

    （1）求这个二次函数的解析式；

    （2）若点C（m，0）（m＞2）在这个二次函数的图象上，连接AB，BC，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案