
【题目】晚上,小亮走在大街上发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3m,左边的影子长为1.5m,又知自己身高1.80m,两盏路灯的高相同,两盏路灯之间的距离为12m,则路灯的高为( )

A. 6.6m B. 6.7m C. 6.8m D. 6.9m
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣ax+1=0有两个相等的实数根,且该实数根也是关于x的方程![]() =
=![]() 的根,则ba的值为( )
的根,则ba的值为( )
A. ![]() B. ﹣
B. ﹣![]() C. 9 D. ﹣9
C. 9 D. ﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
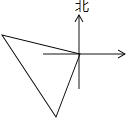
【题目】某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )
A. 南偏东![]() ,
,![]() 千米 B. 北偏西
千米 B. 北偏西![]() ,
,![]() 千米
千米
C. 南偏东![]() ,100千米 D. 北偏西
,100千米 D. 北偏西![]() ,100千米
,100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
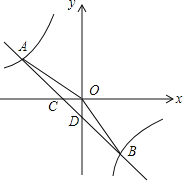
【题目】如图,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=
的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源: 题型:
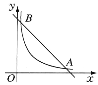
【题目】如图,在直角坐标系中,直线y=6-x与双曲线y=![]() (x>0)的图象相交于点A,B,设点A的坐标为(m,n),那么以m为长、n为宽的矩形的面积和周长分别为( )
(x>0)的图象相交于点A,B,设点A的坐标为(m,n),那么以m为长、n为宽的矩形的面积和周长分别为( )
A. 4,6 B. 4,12 C. 8,6 D. 8,12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com