
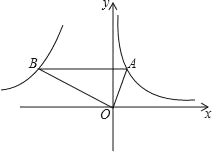
【题目】如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=![]() ,则经过点B(x,y)的反比例函数解析式为( )
,则经过点B(x,y)的反比例函数解析式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,无论k取何实数,直线y=(k-1)x+4-5k总经过定点P,则点P与动点Q(5m-1,5m+1)的距离的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
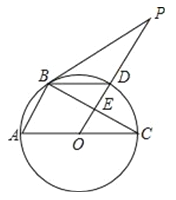
【题目】如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
(1)求证:BD平分∠PBC;
(2)若PD =3DE,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)
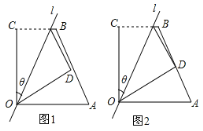
如图1,四边形OABC中,OA=a,OC=8,BC=6,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,8];
(尝试)
(1)若点D与OA的中点重合,则这个操作过程为FZ[____,____];
(2)若点D恰为AB的中点(如图2),求θ的值;
(应用)
经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,直线l与AB相交于点F,试画出图形并解决下列问题:
①求出a的值;
②若P为边OA上一动点,连接PE、PF,请直接写出PE+PF的最小值.
(备注:等腰直角三角形的三边关系满足![]() 或
或![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
10 | 10 | 500 |
15 | 20 | 900 |
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
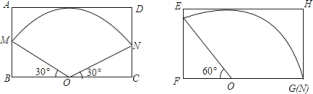
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华的爸爸要用一块矩形铁皮加工出一个底面半径为![]() ,高为
,高为![]() 的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
![]() 你能求出这个锥形漏斗的侧面展开图的圆心角吗?
你能求出这个锥形漏斗的侧面展开图的圆心角吗?
![]() 如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
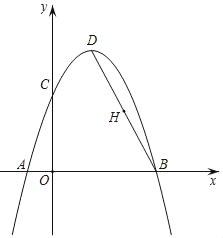
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .
(注:抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣![]() ,顶点坐标为(﹣
,顶点坐标为(﹣![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com