
【题目】在平面直角坐标系中,抛物线与直线均过原点,直线经过抛物线的顶点(2,4),则下列说法:①当0<x<2时,y2>y1;②y2随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在; ④若y2=2,则x=2﹣![]() 或x=1.
或x=1.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角![]() 为
为![]() ,窗户的一部分在教室地面所形成的影长
,窗户的一部分在教室地面所形成的影长![]() 为
为![]() 米,窗户的高度
米,窗户的高度![]() 为
为![]() 米.求窗外遮阳蓬外端一点
米.求窗外遮阳蓬外端一点![]() 到教室窗户上椽的距离
到教室窗户上椽的距离![]() .(参考数据:
.(参考数据:![]() ,结果精确
,结果精确![]() 米)
米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
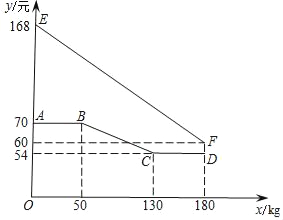
【题目】绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c(b,c均为常数)的图象经过两点A(2,0),B(0,﹣6).
(1)求这个二次函数的解析式;
(2)若点C(m,0)(m>2)在这个二次函数的图象上,连接AB,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
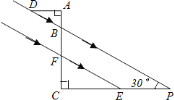
【题目】如图,河流两岸![]() 、
、![]() 平行,
平行,![]() 、
、![]() 是河岸
是河岸![]() 上间隔
上间隔![]() 米的两根电线杆,某人在河岸
米的两根电线杆,某人在河岸![]() 上的
上的![]() 处测得
处测得![]() ,然后沿河岸走了
,然后沿河岸走了![]() 米到达
米到达![]() 处,测得
处,测得![]() ,则河流的宽度
,则河流的宽度![]() 的值为________
的值为________![]() (结果精确到个位,
(结果精确到个位,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
科目:初中数学 来源: 题型:
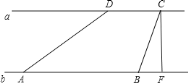
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com