
【题目】绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
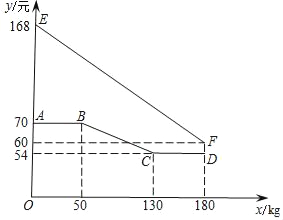
【答案】(1) 产品销售价y1(元)与产量x(kg)之间的函数关系式为y1=﹣![]() x+168(0≤x≤180);(2) y2=
x+168(0≤x≤180);(2) y2= ;(3) 该产品产量为110kg时,获得的利润最大,最大值为4840元
;(3) 该产品产量为110kg时,获得的利润最大,最大值为4840元
【解析】
(1)根据线段EF经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(2)显然,当0≤x≤50时,y2=70;当130≤x≤180时,y2=54;当50<x<130时,设y2与x之间的函数关系式为y2=mx+n,利用待定系数法确定一次函数的表达式即可;
(3)利用:总利润=每千克利润×产量,根据x的取值范围列出有关x的二次函数,求得最值比较可得.
(1)设y1与x之间的函数关系式为y1=kx+b,
∵经过点(0,168)与(180,60),
∴![]() ,解得:
,解得: ,
,
∴产品销售价y1(元)与产量x(kg)之间的函数关系式为y1=-![]() x+168(0≤x≤180);
x+168(0≤x≤180);
(2)由题意,可得当0≤x≤50时,y2=70;
当130≤x≤180时,y2=54;
当50<x<130时,设y2与x之间的函数关系式为y2=mx+n,
∵直线y2=mx+n经过点(50,70)与(130,54),
∴![]() ,解得
,解得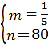 .
.
∴当50<x<130时,y2=-![]() x+80.
x+80.
综上所述,生产成本y2(元)与产量x(kg)之间的函数关系式为y2=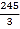 ;
;
(3)设产量为xkg时,获得的利润为W元,
①当0≤x≤50时,W=x(-![]() x+168-70)=-
x+168-70)=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴当x=50时,W的值最大,最大值为3400;
②当50<x<130时,W=x[(-![]() x+168)-(-
x+168)-(-![]() x+80)]=-
x+80)]=- ![]() (x-110)2+4840,
(x-110)2+4840,
∴当x=110时,W的值最大,最大值为4840;
③当130≤x≤180时,W=x(-![]() x+168-54)=-
x+168-54)=-![]() (x-95)2+5415,
(x-95)2+5415,
∴当x=130时,W的值最大,最大值为4680.
因此当该产品产量为110kg时,获得的利润最大,最大值为4840元.


科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧![]() 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.
(1)求证:AP=BQ;
(2)当BQ=4![]() 时,求扇形COQ的面积及
时,求扇形COQ的面积及![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )

A. ![]() (m2﹣4) B.
(m2﹣4) B. ![]() m2﹣2 C.
m2﹣2 C. ![]() (4﹣m2) D. 2﹣
(4﹣m2) D. 2﹣![]() m2
m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
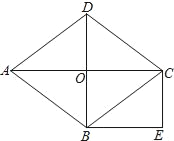
【题目】如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.

查看答案和解析>>
科目:初中数学 来源: 题型:
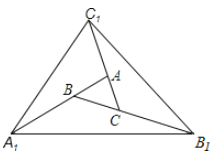
【题目】如图,对面积为S的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;··· ;则![]() ______. 按此规律继续下去,可得到
______. 按此规律继续下去,可得到![]() ,则其面积
,则其面积![]() _______.
_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com