
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.

【答案】【感知】![]() ;【拓展】AG=
;【拓展】AG=![]() ;【探究】当 AG=CH=
;【探究】当 AG=CH=![]() ,BE=DF=1 时,直线 EF、GH 把四边形 ABCD 的面积四等分.
,BE=DF=1 时,直线 EF、GH 把四边形 ABCD 的面积四等分.
【解析】
感知:如图①,根据正方形的性质和全等三角形的性质即可得到结论;
拓展:如图②,过O作ON⊥AD于N,OM⊥AB于M,根据图形的面积得到![]() mb=
mb= ![]() AGa,于是得到结论;
AGa,于是得到结论;
探究:如图③,过O作KL⊥AB,PQ⊥AD,则KL=2OK,PQ=2OQ,根据平行四边形的面积公式得到![]() =
= ![]() ,根据三角形的面积公式列方程即可得到结论.
,根据三角形的面积公式列方程即可得到结论.
感知:如图①,
∵四边形ABCD是正方形,
∴∠OAG=∠OBE=45°,OA=OB,
在△AOG与△BOE中, ,
,
∴△AOG≌△BOE,
∴S四边形AEOG=S△AOB=![]() S正方形 ABCD;
S正方形 ABCD;
故答案为:![]() ;
;
拓展:如图②,过O作ON⊥AD于 N,OM⊥AB于M,

∵S△AOB=![]() S矩形ABCD,S四边形AEOG=
S矩形ABCD,S四边形AEOG=![]() S矩形ABCD,
S矩形ABCD,
∴S△AOB=S四边形AEOG,
∵S△AOB=S△BOE+S△AOE,S四边形AEOG=S△AOG+S△AOE,
∴S△BOE=S△AOG,
∵S△BOE=![]() BEOM=
BEOM=![]() m·
m·![]() b=
b=![]() mb,S△AOG=
mb,S△AOG=![]() AGON=
AGON=![]() AG
AG![]() a=
a=![]() AGa,
AGa,
∴![]() mb=
mb=![]() AGa,
AGa,
∴AG=![]() ;
;
探究:如图③,过O作KL⊥AB,PQ⊥AD,
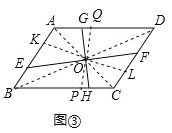
则 KL=2OK,PQ=2OQ,
∵S平行四边形ABCD=ABKL=ADPQ,
∴3×2OK=5×2OQ,
∴![]() =
=![]() ,
,
∵S△AOB=![]() S平行四边形ABCD,S四边形AEOG=
S平行四边形ABCD,S四边形AEOG=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△BOE=S△AOG,
∵S△BOE=![]() BEOK=
BEOK=![]() ×1×OK,S△AOG=
×1×OK,S△AOG=![]() AGOQ,
AGOQ,
∴![]() ×1×OK=
×1×OK=![]() AGOQ,
AGOQ,
∴![]() =AG=
=AG=![]() ,
,
∴当AG=CH=![]() ,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.
,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,△ABC≌△DEF,AM、DN分别是△ABC和△DEF的角平分线,

(1)求证:AM=DN
(2)其他两对应角的角平分线也有此结果吗?它们有什么规律,请用一句话表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,CE 平分∠ACD,AE 平分∠BAC,且∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图 2,若∠E=90°且 AB 与 CD 的位置关系保持不变,当直角顶点 E 移动时,写出∠BAE 与∠ECD 的数量关系,并说明理由;
(3)如图 3,P 为线段 AC 上一定点,点 Q 为直线 CD 上一动点,且 AB 与 CD 的位置 关系保持不变,当点 Q 在射线 CD 上运动时(不与点 C 重合),∠PQD,∠APQ 与∠ BAC 有何数量关系?写出结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.

(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知小华家、小夏家、小红家及学校在同一条大路旁,一天,他们放学后从学校出发,先向南行1000m到达小华家A处,继续向北行3000m到达小红B家处,然后向南行6000m到小夏家C处.
(1)以学校以原点,以向南方向为正方向,用1个单位长度表示1000m,请你在数轴上表示出小华家、小夏家、小红家的位置;
(2)小红家在学校什么位置?离学校有多远?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l1与直线l2平行,且它们之间的距离为3,A,B是直线l1上的两个定点,C,D是直线l2上的两个动点(点C在点D的左侧),AB=CD=6,连接AC、BD、BC,将△ABC沿BC折叠得到△A1BC.(如图1)
(1)当A1与D重合时(如图2),四边形ABDC是什么特殊四边形,为什么?
(2)当A1与D不重合时,连接A1D,则A1 D∥BC(不需证明),此时若以A1,B,C,D为顶点的四边形为矩形,且矩形的边长分别为a,b,求(a+b)2的值.
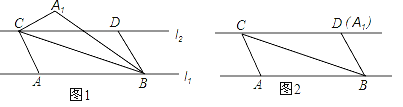
查看答案和解析>>
科目:初中数学 来源: 题型:
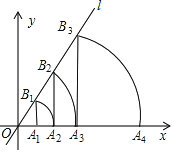
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
查看答案和解析>>
科目:初中数学 来源: 题型:
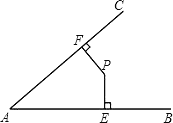
【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com