
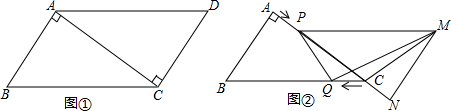
���� ��1�����ݹ��ɶ������AC������PQ��AB���ó�$\frac{CP}{CA}$=$\frac{CQ}{CB}$��$\frac{4-t}{4}$=$\frac{t}{5}$����⼴�ɣ�
��2������P��PE��BC��E�����ݡ�CPE�ס�CBA���ó�$\frac{4-t}{5}$=$\frac{PE}{3}$�����PE=$\frac{12}{5}$-$\frac{3}{5}$t���ٸ���S��QMC=S��QPC���ó�y=S��QMC=$\frac{1}{2}$QC•PE���ٴ�����㼴�ɣ�
��3������S��QMC��S�ı���ABQP=1��4���ó�S��QPC��S��ABC=1��5������ó���$\frac{6}{5}$t-$\frac{3}{10}$t2����6=1��5���ټ��㼴�ɣ�
��4������PQ��MQ�ó���PEQ�ס�MQP���ó�PQ2=MP•EQ�����ݹ��ɶ����ó�PE2+EQ2=MP•EQ���ٷֱ����ó���$\frac{12-3t}{5}$��2+��$\frac{16-9t}{5}$��2=5��$\frac{16-9t}{5}$�����t���ɣ�
��� �⣺��1����Rt��ABC�У�AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4��
��ƽ�Ƶ����ʵ�MN��AB��
��PQ��MN��
��PQ��AB��
��$\frac{CP}{CA}$=$\frac{CQ}{CB}$��
��$\frac{4-t}{4}$=$\frac{t}{5}$��
t=$\frac{20}{9}$��
��2������P��PE��BC��E����ͼ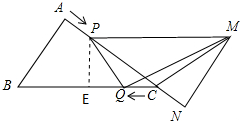
�ߡ�CPE�ס�CBA��
��$\frac{CP}{CB}$=$\frac{PE}{BA}$��
��$\frac{4-t}{5}$=$\frac{PE}{3}$��
��PE=$\frac{12}{5}$-$\frac{3}{5}$t��
��PE��BC��
��S��QMC=S��QPC��
��y=S��QMC=$\frac{1}{2}$QC•PE=$\frac{1}{2}$t��$\frac{12}{5}$-$\frac{3}{5}$t��=$\frac{6}{5}$t-$\frac{3}{10}$t2��0��t��4����
��3����S��QMC��S�ı���ABQP=1��4��
��S��QPC��S�ı���ABQP=1��4��
��S��QPC��S��ABC=1��5��
�ࣨ$\frac{6}{5}$t-$\frac{3}{10}$t2����6=1��5��
��t=2��
��4����PQ��MQ��
���PQM=��PEQ��
�ߡ�MPQ=��PQE��
���PEQ�ס�MQP��
��$\frac{PQ}{MP}$=$\frac{EQ}{PQ}$��
��PQ2=MP•EQ��
��PE2+EQ2=MP•EQ��
��CE=$\frac{16-4t}{5}$��
��EQ=CE-CQ=$\frac{16-4t}{5}$-t=$\frac{16-9t}{5}$��
�ࣨ$\frac{12-3t}{5}$��2+��$\frac{16-9t}{5}$��2=5��$\frac{16-9t}{5}$��
��t1=0����ȥ����t2=$\frac{3}{2}$��
��t=$\frac{3}{2}$ʱ��PQ��MQ��
���� ���⿼�����������ۺϣ��õ���֪ʶ�������������ε��ж������ʡ����ɶ�����ƽ���ߵ����ʡ������ε�������ؼ��Ǹ������⻭��ͼ�Σ����������ߣ��������������Σ�


 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
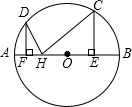 ��ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O�ϵ����㣬����C��CE��AB�ڵ�E������D��DF��AB�ڵ�F��HΪEF�ϵ�����һ�㣬��AB=10��CE=4��DF=3����CH+DH����Сֵ��7$\sqrt{2}$��
��ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O�ϵ����㣬����C��CE��AB�ڵ�E������D��DF��AB�ڵ�F��HΪEF�ϵ�����һ�㣬��AB=10��CE=4��DF=3����CH+DH����Сֵ��7$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
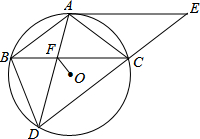 ��ͼ����ABC�ڽ��ڡ�O��AB=AC��BDΪ��O���ң���AB��CD������A����O������AE��DC���ӳ��߽��ڵ�E��AD��BC���ڵ�F��
��ͼ����ABC�ڽ��ڡ�O��AB=AC��BDΪ��O���ң���AB��CD������A����O������AE��DC���ӳ��߽��ڵ�E��AD��BC���ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
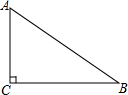 ��ͼ����֪��ABC����C=Rt�ϣ�AC��BC��DΪBC��һ�㣬�ҵ�A��B����ľ�����ȣ�
��ͼ����֪��ABC����C=Rt�ϣ�AC��BC��DΪBC��һ�㣬�ҵ�A��B����ľ�����ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-10% | B�� | a•10% | C�� | a��1-10%�� | D�� | a��1+10%�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-2 | B�� | x��2 | C�� | x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��0�� | B�� | ��3��0�� | C�� | ��-3��0�� | D�� | ��0��-4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��-1 | B�� | k��-1 | C�� | k��0 | D�� | k��1��k��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com