
已知某市2014年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2014年10月份的水费为620元,求该企业2014年10月份的用水量;
(3)为鼓励企业节约用水,该市自2015年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2014年收费标准收取水费外,超过80吨的部分每吨另加收
 元的污水处理费,若某企业2015年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2015年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.

【考点】一次函数的应用.
【分析】(1)设y关于x的函数关系式y=kx+b,然后利用待定系数法求一次函数解析式解答;
(2)把水费620元代入函数关系式解方程即可;
(3)利用水费+污水处理费=600元,列出方程解决问题.
【解答】解:(1)设y关于x的函数关系式y=kx+b,则
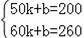
 ,
,
解得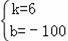
 ,
,
所以,y关于x的函数关系式是y=6x﹣100;
(2)由图可知,当y=620时,x>50,
所以,6x﹣100=620,
解得x=120,
答:该企业2013年10月份的用水量为120吨;
(3)由题意得6x﹣100+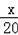
 (x﹣80)=600,
(x﹣80)=600,
化简得:x2+40x﹣14000=0,
解得:x1=100,x2=﹣140(不合题意,舍去),
答:这个企业2015年3月份的用水量是100吨.
【点评】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知函数值求自变量.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
A.π B.2π C. D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
某班组织活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品.已知笔记本2元/本,中性笔1元/支,且每种奖品至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的中性笔数量多于笔记本数量的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针.若针扎到小正方形(阴影部分)的概率是
 ,则大、小两个正方形的边长之比是 .
,则大、小两个正方形的边长之比是 .


查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com