
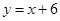 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.
 (2)证明:在等腰直角三角形APD中,
(2)证明:在等腰直角三角形APD中, ,DA=DP,
,DA=DP, ,∴DP⊥AD于D,由(1)可得
,∴DP⊥AD于D,由(1)可得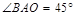 ,∴
,∴ ,又∵PG⊥x轴于G,∴PG = PD,∴
,又∵PG⊥x轴于G,∴PG = PD,∴ ,∴
,∴ ,∴
,∴ ,即
,即 ,又∵PQ⊥PF,∴
,又∵PQ⊥PF,∴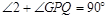 ,∴
,∴ ,在△PGF和△PDQ中,
,在△PGF和△PDQ中, ,
, ,
, ,∴△PGF≌△PDQ,∴PF=PQ(3)
,∴△PGF≌△PDQ,∴PF=PQ(3) OP⊥DP,OP=DP 证明:延长DP至H,使得PH=PD,∵P为BE的中点,∴PB=PE,在△PBH和△PED中,
OP⊥DP,OP=DP 证明:延长DP至H,使得PH=PD,∵P为BE的中点,∴PB=PE,在△PBH和△PED中, ,
, ,
, ,∴△PBH≌△PED,∴BH=ED,∴
,∴△PBH≌△PED,∴BH=ED,∴ ,∴BH∥ED,在等腰直角三角形ADE中,AD=ED,
,∴BH∥ED,在等腰直角三角形ADE中,AD=ED, ,∴AD=BH,
,∴AD=BH, ,∴DE∥x轴,BH∥x轴, BH⊥y轴,∴
,∴DE∥x轴,BH∥x轴, BH⊥y轴,∴ ,由(1)可得 OA=OB,在△DAO和△HBO中,
,由(1)可得 OA=OB,在△DAO和△HBO中, ,
, ,
, ,∴△DAO≌△HBO,∴OD=OH,∠5=∠6,∵
,∴△DAO≌△HBO,∴OD=OH,∠5=∠6,∵ ∴
∴ ,∴在等腰直角三角形△DOH中,∵DP=HP,∴OP⊥DP,
,∴在等腰直角三角形△DOH中,∵DP=HP,∴OP⊥DP, ,∴
,∴ ,∴OP=PD
,∴OP=PD 直线
直线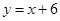 与x轴交于点A,与y轴交于点B,∴A(-6,0),B(0,6),∴OA=OB,∴
与x轴交于点A,与y轴交于点B,∴A(-6,0),B(0,6),∴OA=OB,∴ ,在△AOB中,
,在△AOB中, ,∴
,∴
 ,DA=DP,
,DA=DP, 推出DP⊥AD,再利用(1)中的结论,结合图像,以及全等三角形的判定,可以推出,∴PF=PQ。
推出DP⊥AD,再利用(1)中的结论,结合图像,以及全等三角形的判定,可以推出,∴PF=PQ。 ,所以利用全等三角形的判定定理,推出△DAO≌△HBO,同时利用等腰直角三角形的特殊性,可以推出OP=PD
,所以利用全等三角形的判定定理,推出△DAO≌△HBO,同时利用等腰直角三角形的特殊性,可以推出OP=PD

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源:不详 题型:解答题
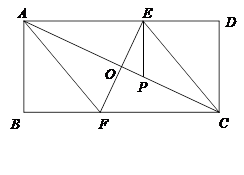
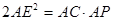 ,求证:CD∥PE.
,求证:CD∥PE.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
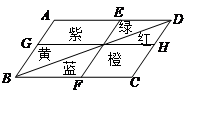
| A.红花,绿花种植面积一定相等 |
| B.紫花,橙花种植面积一定相等 |
| C.红花,蓝花种植面积一定相等 |
| D.蓝花,黄花种植面积一定相等 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com