
،¾جâؤ؟،؟بçح¼£¬ئ½أوض±½ا×ّ±êدµضذ£¬ABCDخھ³¤·½ذخ£¬ئنضذµمA،¢C×ّ±ê·ض±ًخھ£¨©پ4£¬2£©،¢£¨1£¬©پ4£©£¬ازAD،خxضل£¬½»yضلسعMµم£¬AB½»xضلسعN£®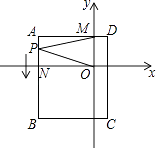
£¨1£©اَB،¢Dء½µم×ّ±ê؛ح³¤·½ذخABCDµؤأو»£»
£¨2£©ز»¶¯µمP´سA³ِ·¢£¬زش ![]() ¸ِµ¥خ»/أëµؤثظ¶برطABدٍBµمشث¶¯£¬شعPµمشث¶¯¹³جضذ£¬ء¬½سMP،¢OP£¬اëض±½سذ´³ِ،دAMP،¢،دMPO،¢،دPONض®¼نµؤتء؟¹طدµ£»
¸ِµ¥خ»/أëµؤثظ¶برطABدٍBµمشث¶¯£¬شعPµمشث¶¯¹³جضذ£¬ء¬½سMP،¢OP£¬اëض±½سذ´³ِ،دAMP،¢،دMPO،¢،دPONض®¼نµؤتء؟¹طدµ£»
£¨3£©تا·ٌ´وشعؤ³ز»ت±؟جt£¬ت¹ب½اذخAMPµؤأو»µبسع³¤·½ذخأو»µؤ ![]() £؟بô´وشع£¬اَtµؤضµ²¢اَ´ثت±µمPµؤ×ّ±ê£»بô²»´وشعثµأ÷ہيسة£®
£؟بô´وشع£¬اَtµؤضµ²¢اَ´ثت±µمPµؤ×ّ±ê£»بô²»´وشعثµأ÷ہيسة£®
،¾´ً°¸،؟
£¨1£©
½â£؛،كµمA،¢C×ّ±ê·ض±ًخھ£¨©پ4£¬2£©،¢£¨1£¬©پ4£©£¬
¶ّثؤ±كذخABCDخھ¾طذخ£¬
،àB£¨©پ4£¬©پ4£©£¬D£¨1£¬2£©£»
¾طذخABCDµؤأو»=£¨1+4£©،ء£¨2+4£©=30
£¨2£©
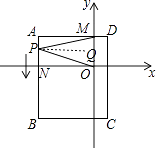
½â£؛µ±µمPشعدك¶خANةدت±£¬×÷PQ،خAM£¬بçح¼£¬
،كAM،خON£¬
،àAM،خPQ،خON£¬
،à،دQPM=،دAMP£¬،دQPO=،دPON£¬
،à،دQPM+،دQPO=،دAMP+،دPON£¬
¼´،دMPO=،دAMP+،دPON£»
µ±µمPشعدك¶خNBةدت±£¬ح¬رù·½·¨؟ةµأ،دMPO=،دAMP©پ،دPON
£¨3£©
½â£؛´وشع£®
،كAM=4£¬AP= ![]() t£¬
t£¬
،àS،÷AMP= ![]() ،ء4،ء
،ء4،ء ![]() t=t£¬
t=t£¬
،كب½اذخAMPµؤأو»µبسع³¤·½ذخأو»µؤ ![]() £¬
£¬
،àt=30،ء ![]() =10£¬
=10£¬
،àAP= ![]() ،ء10=5£¬
،ء10=5£¬
،كAN=2£¬
،àPµم×ّ±êخھ£¨©پ4£¬©پ3£©£®
،¾½âخِ،؟£¨1£©ہûسأµمA،¢Cµؤ×ّ±ê؛ح¾طذخµؤذشضتز×µأB£¨©پ4£¬©پ4£©£¬D£¨1£¬2£©£¬ب»؛َ¸ù¾ف¾طذخأو»¹«ت½¼ئثم¾طذخABCDµؤأو»£»£¨2£©·ضہàجضآغ£؛µ±µمPشعدك¶خANةدت±£¬×÷PQ،خAM£¬بçح¼£¬ہûسأئ½ذذدكµؤذشضتز×µأ،دQPM=،دAMP£¬،دQPO=،دPON£¬شٍ،دMPO=،دAMP+،دPON£»µ±µمPشعدك¶خNBةدت±£¬ح¬رù·½·¨؟ةµأ،دMPO=،دAMP©پ،دPON£»£¨3£©سةسعAM=4£¬AP= ![]() t£¬¸ù¾فب½اذخأو»¹«ت½µأµ½S،÷AMP=t£¬شظہûسأب½اذخAMPµؤأو»µبسع³¤·½ذخأو»µؤ
t£¬¸ù¾فب½اذخأو»¹«ت½µأµ½S،÷AMP=t£¬شظہûسأب½اذخAMPµؤأو»µبسع³¤·½ذخأو»µؤ ![]() ؟ة¼ئثم³ِt=10£¬شٍAP=5£¬ب»؛َ¸ù¾فµمµؤ×ّ±êµؤ±يت¾·½·¨ذ´³ِPµم×ّ±ê£®
؟ة¼ئثم³ِt=10£¬شٍAP=5£¬ب»؛َ¸ù¾فµمµؤ×ّ±êµؤ±يت¾·½·¨ذ´³ِPµم×ّ±ê£®
،¾؟¼µم¾«خِ،؟¸ù¾فجâؤ؟µؤزرضھجُ¼£¬ہûسأب½اذخµؤأو»µؤدà¹طضھت¶؟ةزشµأµ½ختجâµؤ´ً°¸£¬ذèزھصئخصب½اذخµؤأو»=1/2،ءµ×،ء¸ك£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟أüجâ،°بç¹ûa2£½b2£¬ؤاأ´|a|£½|b|،±µؤؤوأüجâتا________________________£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ض±دك![]() سëxضل£¬yضل·ض±ً½»سعA£¬Bء½µم£¬µمA¹طسعض±دك
سëxضل£¬yضل·ض±ً½»سعA£¬Bء½µم£¬µمA¹طسعض±دك![]() µؤ¶ش³ئµمخھµمC£®
µؤ¶ش³ئµمخھµمC£®
£¨1£©اَµمCµؤ×ّ±ê£»
£¨2£©بôإ×خïدك![]() ¾¹A£¬B£¬Cبµم£¬اَ¸أإ×خïدكµؤ±ي´ïت½£»
¾¹A£¬B£¬Cبµم£¬اَ¸أإ×خïدكµؤ±ي´ïت½£»
£¨3£©بôإ×خïدك![]() ¾¹A£¬Bء½µم£¬از¶¥µمشعµع¶دَدق£¬إ×خïدكسëدك¶خACسذء½¸ِ¹«¹²µم£¬اَaµؤب،ضµ·¶خ§£®
¾¹A£¬Bء½µم£¬از¶¥µمشعµع¶دَدق£¬إ×خïدكسëدك¶خACسذء½¸ِ¹«¹²µم£¬اَaµؤب،ضµ·¶خ§£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬µمP،¢Qتا·´±بہ؛¯تy= ![]() ح¼دٌةدµؤء½µم£¬PA،حyضلسعµمA£¬QN،حxضلسعµمN£¬×÷PM،حxضلسعµمM£¬QB،حyضلسعµمB£¬ء¬½سPB،¢QM£¬،÷ABPµؤأو»¼اخھS1 £¬ ،÷QMNµؤأو»¼اخھS2 £¬ شٍS1S2 £® £¨جî،°£¾،±»ٍ،°£¼،±»ٍ،°=،±£©
ح¼دٌةدµؤء½µم£¬PA،حyضلسعµمA£¬QN،حxضلسعµمN£¬×÷PM،حxضلسعµمM£¬QB،حyضلسعµمB£¬ء¬½سPB،¢QM£¬،÷ABPµؤأو»¼اخھS1 £¬ ،÷QMNµؤأو»¼اخھS2 £¬ شٍS1S2 £® £¨جî،°£¾،±»ٍ،°£¼،±»ٍ،°=،±£© 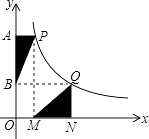
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعز»¸±ب½ا°هABC؛حDECضذ£¬،دACB=،دCDE=90،م£¬،دBAC=60،م£¬،دDEC=45،م£® 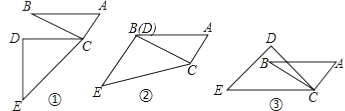
£¨1£©µ±AB،خDCت±£¬بçح¼¢ظ£¬اَ،دDCBµؤ¶بت£®
£¨2£©µ±CDسëCBضط؛دت±£¬بçح¼¢ع£¬إذ¶دDEسëACµؤخ»ضأ¹طدµ£¬²¢ثµأ÷ہيسة£®
£¨3£©بçح¼¢غ£¬µ±،دDCBµبسع¶àةظ¶بت±£¬AB،خEC£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬AB،خCD£¬ض±دكMN·ض±ً½»AB،¢CDسعµمE£¬F£¬EGئ½·ض،دAEF£¬EG،حFGسعµمG£¬بô،دBEM=60،م£¬شٍ،دCFG= £® 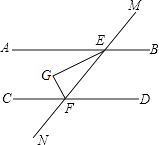
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟2015ؤê10شآ£®خز¹ْ±¾حء؟ئر§¼زحہكدكدبظ»ٌإµ±´¶ûةْہير§»ٍز½ر§½±£¬ث´´ضئذآذح؟¹إ±ز©اàفïثطخھبثہà×÷³ِءثح»³ِ¹±د×£®إ±ش³وشçئعئع×جرّجهµؤض±¾¶ش¼خھ0.00000122أ×£¬صâ¸ِت×ضسأ؟ئر§¼ات·¨±يت¾خھ،، ،،أ×£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ¹طسعxµؤ·½³جx2+kx+3=0µؤز»¸ِ¸ùتا ¨C 1£¬شٍk=_______________.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ¶´خ؛¯تy£½2(x£3)2£«1.دآءذثµ·¨£؛
¢ظئنح¼دَµؤ؟ھ؟عدٍدآ£»¢عئنح¼دَµؤ¶ش³ئضلخھض±x£½3£»¢غئنح¼دَ¶¥µم×ّ±êخھ(3£¬1)£»¢ـµ±x<3£¬yثوxµؤشِ´َ¶ّ¼ُذ،£®
شٍئنضذثµ·¨صب·µؤسذ()
A.1¸ِB.2¸ِC.3¸ِD.4¸ِ
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com