
【题目】如图,已知PA、PB切⊙O于A、B两点,CD切⊙O于E,△PCD的周长为20,sin∠APB=![]() ,则⊙O的半径( )
,则⊙O的半径( )
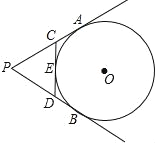
A. 4B. 5C. 6D. 7
【答案】B
【解析】
连接OA、OB、OP,延长BO交PA的延长线于点F.已知PA,PB切⊙O于A、B两点,CD切⊙O于点E,根据切线的性质定理及切线长定理可得∴∠OAF=∠PBF=90°,CA=CE,DB=DE,PA=PB,由△PCD的周长=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=20,可求得PA=PB=10,由sin∠APB=![]() 可得sin∠PFB=
可得sin∠PFB=![]() =
=![]() ,即
,即![]() =
=![]() ,即可求得AF=
,即可求得AF=![]() ,在Rt△AOF中,由tan∠AOF=tan∠BPF=
,在Rt△AOF中,由tan∠AOF=tan∠BPF=![]() =
=![]() 即可求得OA的长.
即可求得OA的长.
连接OA、OB、OP,延长BO交PA的延长线于点F.
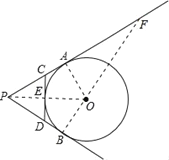
∵PA,PB切⊙O于A、B两点,CD切⊙O于点E
∴∠OAF=∠PBF=90°,CA=CE,DB=DE,PA=PB,
∵△PCD的周长=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=20,
∴PA=PB=10,
∵sin∠APB=![]() ,
,
∴sin∠PFB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:AF=![]() ,
,
在Rt△AOF中,tan∠AOF=tan∠BPF=![]() =
=![]() ,
,
∴![]() ,
,
∴OA=5,
故选B.


科目:初中数学 来源: 题型:
【题目】为积极绘就我市“一福地、四名城”建设的宏伟蓝图,某镇大力发展旅游业,一店铺专门售卖地方特产“曲山老鹅”,以往销售数据表明,该“曲山老鹅”每天销售数量y(只)与销售单价x(元)满足一次函数y=-![]() x+110,每只“曲山老鹅”各项成本合计为20元/只.
x+110,每只“曲山老鹅”各项成本合计为20元/只.
(1)该店铺“曲山老鹅”销售单价x定为多少时,每天获利最大?最大利润是多少?
(2)该店店主关心教育,决定今后的一段时间从每天的销售利润中捐出200元给当地学校作为本学期优秀学生的奖励资金,为了保证该店捐款后每天剩余利润不低于4000元,试确定该“曲山老鹅”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依次规律,则点A8的坐标是_____.
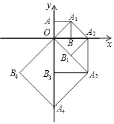
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交线段
交线段![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)在不添加任何辅助线的情况下,请直接写出与![]() 面积相等三角形(不包含
面积相等三角形(不包含![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com