
【题目】如图在直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交线段
交线段![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)在不添加任何辅助线的情况下,请直接写出与![]() 面积相等三角形(不包含
面积相等三角形(不包含![]() )
)
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知PA、PB切⊙O于A、B两点,CD切⊙O于E,△PCD的周长为20,sin∠APB=![]() ,则⊙O的半径( )
,则⊙O的半径( )
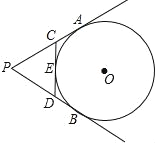
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某品牌的一款学生斜持包,其挎带由单层部分、双层部分和调节扣组成.设单层部分的长度为xcm,双层部分的长度为ycm,经测景,得到如下数据:
x(cm) | 0 | 4 | 6 | 8 | 10 | … | 120 |
y(cm) | M | 58 | 57 | 56 | 55 | … | n |
(1)如图2,在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用平滑曲线连接,并根据图象猜想求出该函数的解析式;
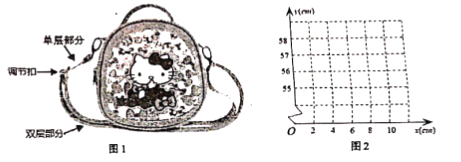
(2)若小花要购买一个持带长为125cm的斜挎包,该款式的斜挎包是否满足小花的需求?请说明理由,(挎带的总长度=单层部分长度+双层部分长度,其中调节扣的长度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
对于线段的垂直平分线我们有如下结论:到线段两个端点距离相等的点在线段的垂直平分线上.即如图①,若PA=PB,则点P在线段AB的垂直平分线上.

请根据阅读材料,解决下列问题:
如图②,直线CD是等边△ABC的对称轴,点D在AB上,点E是线段CD上的一动点(点E不与点C、D重合),连结AE、BE,△ABE经顺时针旋转后与△BCF重合.
(1)旋转中心是点 ,旋转了 (度);
(2)当点E从点D向点C移动时,连结AF,设AF与CD交于点P,在图②中将图形补全,并探究∠APC的大小是否保持不变?若不变,请求出∠APC的度数;若改变,请说出变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,﹣2),OB=4OA,tan∠BCO=2.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M、N分别是线段BC、AB上的动点,点M从点B出发以每秒![]() 个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?
个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
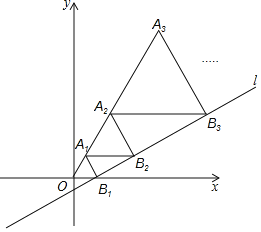
【题目】如图,在平面直角坐标系xOy中,直线l:y=![]() x-
x-![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,按此规律进行下去,则点A3的横坐标为______;点A2018的横坐标为______.
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,按此规律进行下去,则点A3的横坐标为______;点A2018的横坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,抛物线L:y=x2-4x+3与x轴交于A,B两点(点A在点B的左侧),顶点为C.
(1)求点C和点A的坐标.
(2)定义“L双抛图形”:直线x=t将抛物线L分成两部分,首先去掉其不含顶点的部分,然后作出抛物线剩余部分关于直线x=t的对称图形,得到的整个图形称为抛物线L关于直线x=t的“L双抛图形”(特别地,当直线x=t恰好是抛物线的对称轴时,得到的“L双抛图形”不变),
①当t=0时,抛物线L关于直找x=0的“L双抛图形”如图所示,直线y=3与“L双抛图形”有______个交点;
②若抛物线L关于直线x=t的“L双抛图形”与直线y=3恰好有两个交点,结合图象,直接写出t的取值范围:______;
③当直线x=t经过点A时,“L双抛图形”如图所示,现将线段AC所在直线沿水平(x轴)方向左右平移,交“L双抛图形”于点P,交x轴于点Q,满足PQ=AC时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
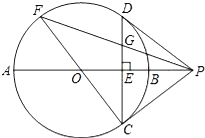
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC=![]() ,求EG的长.
,求EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() 轴相交于点
轴相交于点![]() ,抛物线与
,抛物线与![]() 轴相交于点
轴相交于点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() ,若
,若![]() ,求
,求![]() 的面积;
的面积;

(3)如图2,点![]() 是折线
是折线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,直线
轴,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 落在
落在![]() 轴上,请直接写出
轴上,请直接写出![]() 点的坐标.
点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com