
【题目】如图,AB是⊙O的直径,点C在⊙O上,CE AB于E, CD平分ECB, 交过点B的射线于D, 交AB于F, 且BC=BD.
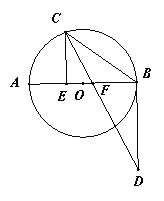
(1)求证:BD是⊙O的切线;
(2)若AE=9, CE=12, 求BF的长.
【答案】(1)证明见解析;(2)10.
【解析】
试题分析:(1)要证明BD是⊙O的切线,由已知条件转化为证明∠DBA=90°即可;
(2)连接AC,利用三角形相似求出BE的值,由勾股定理求出BC的值,由已知条件再证明△EFC∽△BFD,相似三角形的性质利用:对应边的比值相等即可求出BF的长.
试题解析:(1)证明:∵CE⊥AB,
∴∠CEB=90°.
∵CD平分∠ECB,BC=BD,
∴∠1=∠2,∠2=∠D.
∴∠1=∠D,
∴CE∥BD,
∴∠DBA=∠CEB=90°,
∵AB是⊙O的直径,
∴BD是⊙O的切线;
(2)解:连接AC,

∵AB是⊙O直径,
∴∠ACB=90°.
∵CE⊥AB,
∴∠AEC=∠BEC=90°,
∵∠A+∠ABC=90°,∠A+∠ACE=90°,
∴∠ACE=∠ABC,
∴△ACE∽△CBE,
∴![]() ,即CE2=AEEB,
,即CE2=AEEB,
∵AE=9,CE=12,
∴EB=16,
在Rt△CEB中,∠CEB=90,由勾股定理得 BC=20,
∴BD=BC=20,
∵∠1=∠D,∠EFC=∠BFD,
∴△EFC∽△BFD,
∴![]() ,
,
即![]()
∴BF=10.


科目:初中数学 来源: 题型:
【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
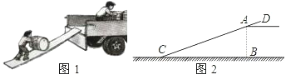
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴的正半轴于点A,点B(
交x轴的正半轴于点A,点B(![]() ,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n=___________.(直接写出答案)
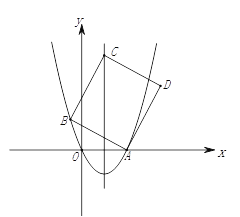
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,动点E、F分别从点C,D出发,以相同速度分别沿CB,DC运动(点E到达C时,两点同时停止运动).连接AE,BF交于点P,过点P分别作PM∥CD,PN∥BC,则线段MN的长度的最小值为( )
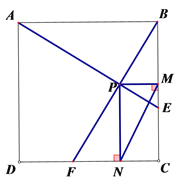
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列题目的解题过程:
已知![]() 为
为![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴![]() 是直角三角形
是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)该步正确的写法应是: ;
(3)本题正确的结论为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题.
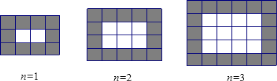
![]() 在第n个图中,第一横行共______ 块瓷砖,第一竖列共有______ 块瓷砖;
在第n个图中,第一横行共______ 块瓷砖,第一竖列共有______ 块瓷砖;![]() 均用含n的代数式表示
均用含n的代数式表示![]()
![]() 设铺设地面所用瓷砖的总块数为y,请写出y与
设铺设地面所用瓷砖的总块数为y,请写出y与![]() 中的n的函数;
中的n的函数;
![]() 按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
![]() 是否存在黑瓷砖与白瓷砖块数相等的情形请通过计算说明理由.
是否存在黑瓷砖与白瓷砖块数相等的情形请通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com