
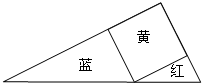
 如图所示,用一张斜边长为30cm的红色直角三角形纸片,一张斜边长为50cm的蓝色直角三角形纸片,一张黄色的正方形纸片,恰好能拼成一个直角三角形,问:红、蓝两张三角形纸片的面积之和是多少?
如图所示,用一张斜边长为30cm的红色直角三角形纸片,一张斜边长为50cm的蓝色直角三角形纸片,一张黄色的正方形纸片,恰好能拼成一个直角三角形,问:红、蓝两张三角形纸片的面积之和是多少?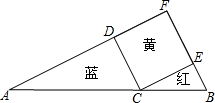 解:∵∠ACD+∠BCE=90°,∠B+∠ECB=90°,
解:∵∠ACD+∠BCE=90°,∠B+∠ECB=90°,| AC |
| BC |
| DC |
| BE |
| AD |
| EC |
| 5 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 11250 |
| 17 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 5 |
| 3 |
| 3 |
| 5 |
| 11250 |
| 17 |


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:
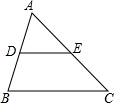 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠C=40°.
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠C=40°.查看答案和解析>>
科目:初中数学 来源: 题型:
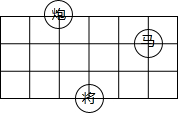 如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )
如图,象棋盘(部分)中,若“马”位置用(0,0)表示,“炮”的位置用(-3,1)表示,则“将”的位置表示为( )| A、(0,0) |
| B、(-2,-2) |
| C、(0,-2) |
| D、(-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | V |
| 3 | V |
| 3 | V |
| 3 | V |
| 3 | 8V |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com