
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() 交
交![]() 于点
于点![]() 分别交
分别交![]() 于点
于点![]()
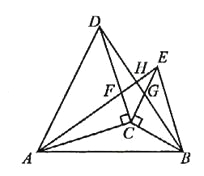
试猜测线段![]() 和
和![]() 的数量和位置关系,并说明理由.
的数量和位置关系,并说明理由.
【答案】![]()
【解析】
由于条件可知CD=AC,BC=CE,且可求得∠ACE=∠DCB,所以△ACE≌△DCB,即AE=BD,∠CAE=∠CDB;又因为对顶角相等即∠AFC=∠DFH,所以∠DHF=∠ACD=90°,即AE⊥BD.
猜测:![]()
理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
又∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB,
在△ACE与△DCB中,
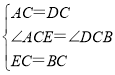
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD.
故线段AE和BD的数量相等,位置是垂直关系.


科目:初中数学 来源: 题型:
【题目】某社区积极响应正在开展的“创文活动”,组织甲、乙两个志愿工程队对社区的一些区域进行绿化改造.已知甲工程队每小时能完成的绿化面积是乙工程队每小时能完成的绿化面积的2倍,并且甲工程队完成300平方米的绿化面积比乙工程队完成300平方米的绿化面积少用3小时,乙工程队每小时能完成多少平方米的绿化面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题;
级别 | A | B | C | D | E | F |
月均用水量x(t) | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | 20<x≤25 | 25<x≤30 |
频数(户) | 6 | 12 | m | 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“全面调查”或“抽样调查);
(2)若将月均用水量的频数绘成形统计图,月均用水量“15<x≤20”组对应的圆心角度数是72°,则本次调查的样本容量是 ,表格中m的值是 ,补全频数分布直方图.
(3)该小区有500户家庭,求该小区月均用水量超过15t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
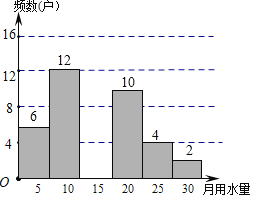
【题目】如图,在△ABC和△DEF中,给出以下六个条件中,以其中三个作为已知条件,不能判断△ABC和△DEF全等的是( ) ①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F;
A.①⑤②B.①②③C.④⑥①D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同﹣直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF。
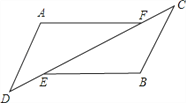
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
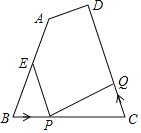
【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com