
【题目】如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证: 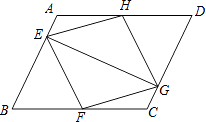
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
【答案】
(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
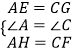 ,
,
∴△AEH≌△CGF(SAS)
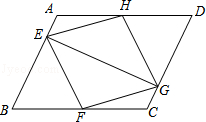
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
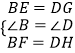
∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形
【解析】(1)由全等三角形的判定定理SAS证得结论;(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.


科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣2x+b的图象与x轴、y轴分别交于B,A两点,与反比例函数y= ![]() (x>0)交于C,D两点.
(x>0)交于C,D两点.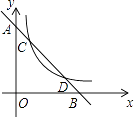
(1)若点D的坐标为(2,m),则m= , b=;
(2)在(1)的条件下,通过计算判断AC与BD的数量关系;
(3)若在一次函数y=﹣2x+b与反比例函数y= ![]() (x>0)的图象第一象限始终有两个交点的前提下,不论b为何值,(2)中AC与BD的数量关系是否恒成立?试说明理由.
(x>0)的图象第一象限始终有两个交点的前提下,不论b为何值,(2)中AC与BD的数量关系是否恒成立?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了顺利通过“国家文明城市”验收,市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完成工程,又能使工程费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC 
(1)求证:BC平分∠PBD;
(2)求证:PC2=PAPB;
(3)若PA=2,PC=2 ![]() ,求阴影部分的面积(结果保留π)
,求阴影部分的面积(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,连接P1P2交OA、OB于E、F,若P1E=![]() ,OP=
,OP=![]() ,则EF的长度是_____.
,则EF的长度是_____.
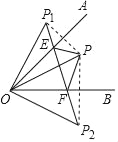
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com