
 如图,在长为10m,宽为8m的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
如图,在长为10m,宽为8m的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
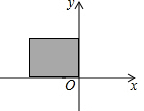 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域,则目标的坐标可能是( )
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域,则目标的坐标可能是( )| A. | (6,-300) | B. | (-3,200) | C. | (8,500) | D. | (-2,-600) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com