
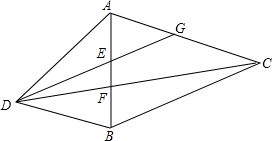
 已知:CA=CB,AG=CG,AE=BE,∠ADB=∠CAB.求证:AF=DF.
已知:CA=CB,AG=CG,AE=BE,∠ADB=∠CAB.求证:AF=DF. 分析 先作出辅助线△ABC的外接圆⊙O,设CD交⊙O于点M,连接OC,BM,OM,OB,OD,EM,由∠ADB=∠CAB=∠ABC,可得出AC,BC是⊙O的切线,由切割线定理及射影定理得出CM•CD=CE•CO,易证O、D、M、E四点共圆,可得△CEM∽△DEO,由射影定理及角的关系可得出△BEM∽△DEB,继而由角的关系可得△BDE∽△BAD,可得出∠BAD=∠ADF,即可得出AF=DF.
解答 证明:如图,作△ABC的外接圆⊙O,设CD交⊙O于点M,连接OC,BM,OM,OB,OD,EM,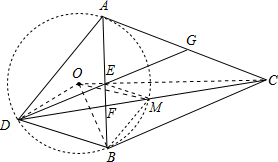
∵CA=CB,
∴∠CAB=∠ABC,
∵∠ADB=∠CAB.
∴∠ADB=∠CAB=∠ABC,
∴AC,BC是⊙O的切线,
∴OC经边点E,BC2=CM•CD,
由射影定理得:BC2=CE•CO,
∴CM•CD=CE•CO,即$\frac{CM}{CO}$=$\frac{CE}{CD}$,
∴△CEM∽△CDO,
∴∠CEM=∠CDO,
∴O、D、M、E四点共圆,
∴∠CME=∠DOE,∠CEM=∠ODM=∠OMD=∠OED,
∴△CEM∽△DEO,
∴EM:OE=CE:DE,即:OE•CE=DE•EM,
由射影定理得:BE2=OE•CE,
∴BE2=DE•EM,即:BE:DE=EM:BE,
∵∠CEM=∠OED,AB⊥OC,
∴∠BEM=∠DEB,
∴△BEM∽△DEB,
∴∠EBM=∠BDE,
∵∠EBM=∠ABM=∠ADM,
∴∠BDE=∠ADM=∠ADF,
∵∠BED=∠AEG=∠BAC=∠ADB,
∴△BDE∽△BAD,
∴∠BAD=∠BDE,
∴∠BAD=∠ADF,
∴AF=DF.
点评 本题主要考查了四点共圆及相似三角形的判定与性质,解题的关键是正确的作出辅助线,灵活运用四点共圆及相似三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在长为10m,宽为8m的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
如图,在长为10m,宽为8m的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com