
���� ��1�����ȷֱ����d��P1��l1����d��l1��l1����d��P2��l1����ֵ���Ƕ��٣��ٰ�������ͣ����d��P1��P2|l1��l1����ֵ�Ƕ��٣�Ȼ��ֱ����d��P1��l1����d��l1��l2����d��P2��l2����ֵ���Ƕ��٣��ٰ�������ͣ����d��P1��P2|l1��l2����ֵ�Ƕ��ټ��ɣ�
��2����������P1A��l3�ڵ�A��P2B��l3�ڵ�B������P1P2��l3�ڵ�C��Ȼ�����P1A+P2B��P1P2���ɵõ�P1P2��l3ʱ��P1A+P2B��ֵ��ݴ����k��ֵ�Ƕ��ټ��ɣ�
��������P1A��l3�ڵ�A��P2B��l3�ڵ�B��P1��P3����ԭ��Գƣ�P3C��l3�ڵ�C��P2P3��l3�ڵ�D��Ȼ�����P2B+P3C��P2P3���ɵõ�P2P3��l3ʱ��P2B+P3Cȡ�����ֵ���ݴ����k��ֵ�Ƕ��ټ��ɣ�
��3��������P1A��l3�ڵ�A��P2B��l4�ڵ�B��Ȼ�����d��P1��P2|l3��l4��=d��P1��l3��+d��l3��l4��+d��P2��l4��=$\sqrt{13}$sin����+�ã�������tan��=$\frac{3\sqrt{3}}{5}$�����ݴ��жϳ�d��P1��P2|l3��l4�������ֵ�Ƕ��ټ��ɣ�
��� �⣺��1����P1��4��0����P2��0��3����l1��y=x��l2��y=$\sqrt{3}$x��
��d��P1��P2|l1��l1��=d��P1��l1��+d��l1��l1��+d��P2��l1��
=$\frac{4}{\sqrt{2}}$+0+$\frac{3}{\sqrt{2}}$
=2$\sqrt{2}+\frac{3}{2}\sqrt{2}$
=$\frac{7}{2}\sqrt{2}$
��d��P1��P2|l1��l2��=d��P1��l1��+d��l1��l2��+d��P2��l2��
=$\frac{4}{\sqrt{2}}$+0+$\frac{|\sqrt{3}��0-1��3|}{\sqrt{{��\sqrt{3}��}^{2}{+��-1��}^{2}}}$
=2$\sqrt{2}+$$\frac{3}{2}$
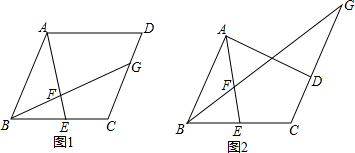
��2������ͼ1����P1A��l3�ڵ�A��P2B��l3�ڵ�B������P1P2��l3�ڵ�C��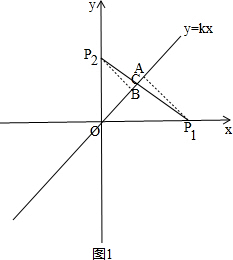 ��
��
d��P1��P2|l3��l3��=d��P1��l3��+d��l3��l3��+d��P2��l3��=P1A+P2B��
��P1A��P1C��P2B��P2C��
��P1A+P2B��P1P2��
�൱P1P2��l3ʱ��
P1A+P2B�����ֵ�ǣ�$\sqrt{{{OP}_{1}}^{2}{+{OP}_{2}}^{2}}=\sqrt{{3}^{2}{+4}^{2}}=5$��
��ʱk=tan��OP2P1=$\frac{{OP}_{1}}{{OP}_{2}}$=$\frac{4}{3}$��
����k��0����d��P1��P2|l3��l3�����ʱ��k=$\frac{4}{3}$��
����ͼ2����P1A��l3�ڵ�A��P2B��l3�ڵ�B��P1��P3����ԭ��Գƣ�P3C��l3�ڵ�C��P2P3��l3�ڵ�D��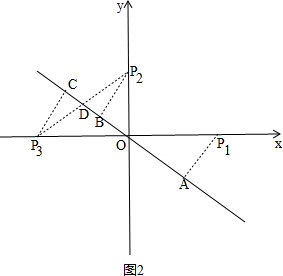 ��
��
��P1��P3����ԭ��Գƣ�
��P1A=P3C��
��d��P1��P2|l3��l3��=d��P1��l3��+d��l3��l3��+d��P2��l3��=P1A+P2B=P2B+P3C��
��P2B��P2D��P3C��P3D��
��P2B+P3C��P2P3��
�൱P2P3��l3ʱ��
P2B+P3C�����ֵ�ǣ�$\sqrt{{{OP}_{3}}^{2}{+{OP}_{2}}^{2}}$=$\sqrt{{4}^{2}{+3}^{2}}$=5��
��ʱk=-tan��OP2P3=-$\frac{{OP}_{3}}{{OP}_{2}}$=-$\frac{4}{3}$��
����k��0����d��P1��P2|l3��l3�����ʱ��k=-$\frac{4}{3}$��
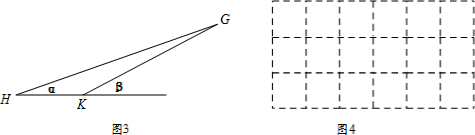
��3����ͼ3����P1A��l3�ڵ�A��P2B��l4�ڵ�B��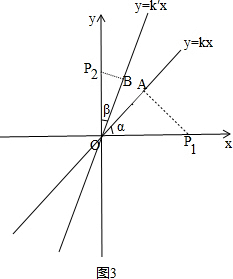 ��
��
���AOP1=������BOP2=�£�
���=90��-30��-��=60��-����
��d��P1��P2|l3��l4��=d��P1��l3��+d��l3��l4��+d��P2��l4��
=P1A+P2B
=OP1sin��+OP2sin��
=4sin��+3sin��
=4sin��+3sin��60��-����
=$\frac{5}{2}$sin��+$\frac{3\sqrt{3}}{2}$cos��
=$\sqrt{13}$sin����+�������tan��=$\frac{3\sqrt{3}}{5}$��
�൱��+��=90�㣬����=90��-arctan$\frac{3\sqrt{3}}{5}$ʱ��
$\sqrt{13}$sin����+�ã������ֵ��$\sqrt{13}$��
��d��P1��P2|l3��l4�������ֵ��$\sqrt{13}$��
�ʴ�Ϊ��$\frac{7}{2}\sqrt{2}$��2$\sqrt{2}+$$\frac{3}{2}$��$\frac{4}{3}$��$\sqrt{13}$��
���� ��1��������Ҫ������һ�κ����ۺ��⣬�����˷����������������������ν��˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������������Ĺؼ�������d��P1��P2|l1��l2��=d��P1��l1��+d��l1��l2��+d��P2��l2�����������
��2��������������Ǻ�������ֵ����Ҫ�������գ�


 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O���߶�AB��ͬһƽ���ڣ�AO=AB=2���Ƶ�O���߶�AB��תһ�ܣ����߶�ABɨ������С���Ϊ4�У�
��ͼ����O���߶�AB��ͬһƽ���ڣ�AO=AB=2���Ƶ�O���߶�AB��תһ�ܣ����߶�ABɨ������С���Ϊ4�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
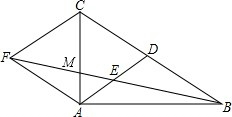 ��ͼ���ڡ�ABC�У���BAC=90�㣬AD��BC���ϵ����ߣ�E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ����ڵ�F��BF��AC�ڵ�M������CF��
��ͼ���ڡ�ABC�У���BAC=90�㣬AD��BC���ϵ����ߣ�E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ����ڵ�F��BF��AC�ڵ�M������CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
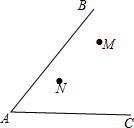 ��ͼ���Ͽ���ѧ�߶��꼶��ѧ���ֱ�������ɽկM��N�����μ����ʱ������Ҫ�ڵ�·AB��AC�γɵ���ǡ�BAC����һ����Ϣ��P��ʹP��������·�ľ�����ȣ�����ʹ��PM=PN������ֱ�ߺ�Բ������P���λ�ã���д������ֵ������ͼ�ۼ�����
��ͼ���Ͽ���ѧ�߶��꼶��ѧ���ֱ�������ɽկM��N�����μ����ʱ������Ҫ�ڵ�·AB��AC�γɵ���ǡ�BAC����һ����Ϣ��P��ʹP��������·�ľ�����ȣ�����ʹ��PM=PN������ֱ�ߺ�Բ������P���λ�ã���д������ֵ������ͼ�ۼ������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com