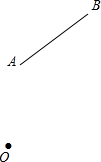练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图，点O与线段AB在同一平面内，AO=AB=2，绕点O将线段AB旋转一周，则线段AB扫过的最小面积为4π．

    分析 当OA⊥AB时，绕点O将线段AB旋转一周，则线段AB扫过的面积最小，根据勾股定理计算出OB，用大圆面积减去小圆面积即可得解．

    解答 解：如图，当OA⊥AB时，绕点O将线段AB旋转一周，则线段AB扫过的面积最小，
    ∵AO=AB=2，
    ∴OB=2$\sqrt{2}$，
    ∴线段AB扫过的最小面积为：π×（2$\sqrt{2}$）2-π×22=4π．
    故答案为：4π．

    点评 本题考查了圆的性质、勾股定理以及圆的面积计算，发现当OA⊥AB时，绕点O将线段AB旋转一周，则线段AB扫过的面积最小是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．设S1=1+$\frac{1}{{1}^{2}}$+$\frac{1}{{2}^{2}}$，S2=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$，S3=1+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$，…，Sn=1+$\frac{1}{{n}^{2}}$+$\frac{1}{（n+1）^{2}}$．
    （1）化简：$\sqrt{{S}_{n}}$（用含n的代数式表示，其中n为正整数）；
    （2）设S=$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$+…+$\sqrt{{S}_{100}}$，求S的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．一组数据中有5个4，5个14，5个24，求这组数据的平均数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知矩形ABCD，AB=4，BD=2．现有另一个与矩形ABCD相似矩形EFGH，相似比为2：1．最初矩形EFGH的GH边放置在∠BCD的平分线处（如图1），现将矩形EFGH 沿着FG作一条直线l，再连接AH、BH、DH、BE，设BC与EH的交点为M，CD与 GH的交点为N（若没有交点则不计），回答下列问题．
    （1）如图1，当矩形ABCD矩形EFGH都不动时，求出矩形ABCD与矩形EFGH重合部分三角形的面积．
    （2）如图2，现矩形ABCD不动，矩形EFGH沿直线l开始出发，以1m/s的速度移动．设移动时间为t，矩形ABCD与矩形EFGH重合部分的面积为S，求出S关于t的函数关系式，并写出相应的取值范围，并且求出当t为多少时，S为最大值？
    （3）如图3，矩形ABCD仍然不动，矩形EFGH运动一段时间后停止在某一个点，并且此时△CEH为等腰三角形，这时，在△AHC中，AH=HC成立吗？请说明理由，并求出此时S和t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．阅读材料：
    ①直线l外一点P到直线l的垂线段的长度，叫做点P到直线l的距离，记作d（P，l）
    ②两条平行线l1，l2，直线上l1任意一点到直线l2的距离，叫做这两条平行线l1，l2之间的距离，记作d（l1，l2）；
    ③若直线l1，l2相交，则定义d（l1，l2）=0
    ④对于同一条直线l，我们定义d（l，l）=0．
    对于两点P1，P2和两条直线l1，l2，定义两点P1，P2的“l1，l2-相关距离”如下：d（P1，P2|l1，l2）=d（P1，l1）+d（l1，l2）+d（P2，l2）
    设P1（4，0），P2（0，3），l1：y=x，l2：y=$\sqrt{3}$x，l3：y=kx，l4：y=k′x，解决以下问题：
    （1）d（P1，P2|l1，l1）=$\frac{7}{2}\sqrt{2}$，d（P1，P2|l1，l2）=2$\sqrt{2}+$$\frac{3}{2}$
    （2）①若k＞0，则当d（P1，P2|l3，l3）最大时，k=$\frac{4}{3}$；
    ②若k＜0，试确定k的值使得d（P1，P2|l3，l3）最大．
    （3）若k′＞k＞0，且，l3，l4的夹角是30°，直接写出d（P1，P2|l3，l4）的最大值$\sqrt{13}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

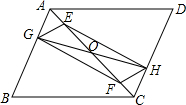    10．如图所示，已知，在?ABCD中，点E，F在AC上，且AF=CE，点G，H分别在AB，CD上，且AG=CH，AC与GH相交于点O，求证：四边形EGFH是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知点B是∠MAN角平分线上一点，∠CBD的两边BC，BD分别与射线AM，AN交于点C，D，且∠MAN+∠CBD=180°．
    （1）如图①，作BE⊥AM于点E，BF⊥AN于点F．若∠MAN=90°，易证：四边形ACBD的面积等于四边形AEBF的面积；
    （2）如图②，图③，作BE⊥AM于点E，BF⊥AN于点F，若0°＜∠MAN＜180°，试探究：四边形ACBD的面积是否等于四边形AEBF的面积，并说明理由；
    （3）如图③，若∠MAN=120°，AC=2，AD=3，直接写出四边形ACBD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

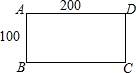    14．据统计资料，甲、乙两种农作物的单位面积产量的比是1：2，现要把一块长为200m，宽100m的长方形土地分为两部分，分别种植这两种作物，使甲、乙两种作物的总产量的比是3：10
    （1）若将原长方形土地分成两部分，其中一种分为长方形，请你设计一种分割方案，并通过计算说明
    （2）若将原长方形土地分成两部分，其中一种分为三角形，请你设计一种分割方案，并通过计算说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解方程组：$\left\{\begin{array}{l}{{a}_{1}+9d=10}\\{{a}_{1}+19d=20}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案