
【题目】如图,六边形ABCDEF的六个角都是120°,边长AB=1cm,BC=3cm,CD=3cm,DE=2cm,则这个六边形的周长是:__.
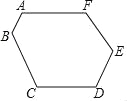
【答案】15cm
【解析】
凸六边形ABCDEF,并不是一规则的六边形,但六个角都是120°,所以通过适当的向外作延长线,可得到等边三角形,进而求解.
解:如图,分别作直线AB、CD、EF的延长线和反向延长线使它们交于点G、H、P.
∵六边形ABCDEF的六个角都是120°,
∴六边形ABCDEF的每一个外角的度数都是60°,
∴△APF、△BGC、△DHE、△GHP都是等边三角形,
∴GC=BC=3cm,DH=DE=2cm,
∴GH=3+3+2=8cm,FA=PA=PG﹣AB﹣BG=8﹣1﹣3=4cm,EF=PH﹣PF﹣EH=8﹣4﹣2=2cm,
∴六边形的周长为1+3+3+2+4+2=15cm.
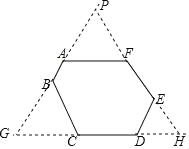
故答案为:15cm.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】元旦期间,某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若房价定为200元时,求宾馆每天的利润;
(2)房价定为多少时,宾馆每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点P为AC的中点,Q从点A运动到B,点Q运动到点B停止,连接PQ,取PQ的中点O,连接OC,OB.
(1)若△ABC∽△APQ,求BQ的长;
(2)在整个运动过程中,点O的运动路径长_____;
(3)以O为圆心,OQ长为半径作⊙O,当⊙O与AB相切时,求△COB的面积.
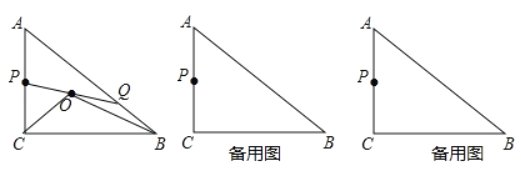
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6![]() ,CE=4,则DE的长为 .
,CE=4,则DE的长为 .
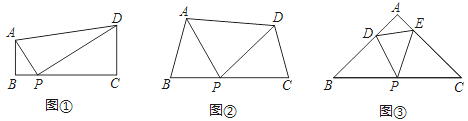
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
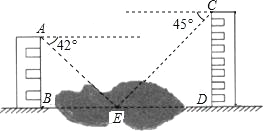
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转一定角度后,BC的对应边B′C交CD边于点G,如果当AB′=B′G时量得AD=7,CG=4,连接BB′、CC′,那么![]() =_____.
=_____.
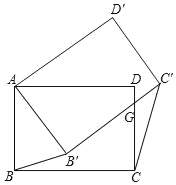
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为( )
,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为( )
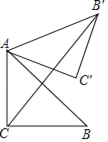
A. ![]() +
+![]() B. 1+
B. 1+![]() C. 3D.
C. 3D. ![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交.当y2≤y3时自变量x的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com