
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB��CD��x�ᣬBC��DE��y�ᣬ��AB=CD=4cm��OA=5cm��DE=2cm������P�ӵ�A��������A��B��C·���˶�����Cֹͣ������Q�ӵ�O��������O��E��D��C·���˶�����Cֹͣ����P��Q����ͬʱ�������ҵ�P���˶��ٶ�Ϊ1cm/s����Q���˶��ٶ�Ϊ2cm/s��
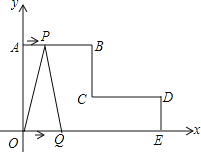
��1��ֱ��д��B��C��D����������ꣻ
��2����P��Q�������![]() sʱ��������PQC�������
sʱ��������PQC�������
��3���������˶���ʱ��Ϊt s����t��ʽ�ӱ�ʾ�˶���������OPQ�����S��
���𰸡���1��B��4��5����C��4��2����D��8��2������2��![]() ����3��S=
����3��S=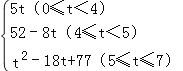 ��
��
��������
�����������1������ƽ��ֱ������ϵд����������꼴�ɣ�
��2���������P��Q�����꣬�����CP��CQ��Ȼ����������ε������ʽ��ʽ���㼴�ɵý⣻
��3���֢�0��t��4ʱ��P��AB�ϣ���Q��OE�ϣ����������������ʽ��ʽ���ɣ�
��4��t��5ʱ����P��BC�ϣ���Q��DE�ϣ�����P��PM��CD��DE���ӳ�����M������S��OPQ=S����OPMB��S��PMQ��S��OEQ����ʽ�������ɣ�
��5��t��7ʱ����P��BC�ϣ���Q��CD�ϣ�����P��PF��CD������Q��QF��OA��PF��F����OE��G��S��OPQ=S����OPFG��S��PFQ��S��OGQ����ʽ�������ɵý⣮
�⣺��1��B��4��5����C��4��2����D��8��2����
��2����t=![]() sʱ����P�˶���·��Ϊ
sʱ����P�˶���·��Ϊ![]() ��
��
��Q�˶���·��Ϊ![]() ��2=11��
��2=11��
���ԣ�P��4��![]() ����Q��7��2����
����Q��7��2����
��CP=![]() ��CQ=3��
��CQ=3��
��S��CPQ=![]() CPCQ=
CPCQ=![]() ��
��![]() ��3=
��3=![]() ��
��
��3��������ã�
�ٵ�0��t��4ʱ������ͼ1��OA=5��OQ=2t��
S��OPQ=![]() OQOA=
OQOA=![]() ��2t��5=5t��
��2t��5=5t��
�ڵ�4��t��5ʱ������ͼ2��OE=8��EM=9��t��PM=4��MQ=17��3t��EQ=2t��8��
S��OPQ=S����OPMB��S��PMQ��S��OEQ��
=![]() ��4+8������9��t����
��4+8������9��t����![]() ��4��17��3t����
��4��17��3t����![]() ��8��2t��8����
��8��2t��8����
=52��8t��
�۵�5��t��7ʱ������ͼ3��PF=14��2t��FQ=7��t��QG=2��OG=18��2t��FG=9��t��
S��OPQ=S����OPFG��S��PFQ��S��OGQ��
=![]() ����14��2t+18��2t������9��t����
����14��2t+18��2t������9��t����![]() ����14��2t����7��t����
����14��2t����7��t����![]() ��18��2t����2��
��18��2t����2��
=t2��18t+77��
����������S=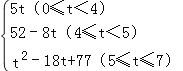 ��
��


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪AB��CD,ֱ��EF�ֱ�AB,CD�ڵ�E,F,EPƽ����BEF,FPƽ����DFE.��˵��:��PEF��ֱ��������.
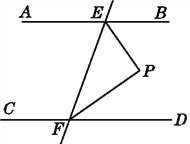
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������DEF��������ABC����ij�ֱ任�õ���ͼ�Σ���A���D����B���E����C���F�ֱ��Ƕ�Ӧ�㣮�۲����������֮��Ĺ�ϵ������������⣺
(1)�ֱ�д����A���D����B���E����C���F�����꣬��˵��������DEF����������ABC���������ı任�õ��ģ�
(2)����Q(a��3��4��b)�ǵ�P(2a��2b��3)ͨ�������任�õ��ģ���a��b��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��һ�����Ͼ���ģ��ABCD����Ϊ10cm����Ϊ4cm�����������㹻���ֱ�����ǰ� PHF ��ֱ�Ƕ���P����AD����(����A��D�غ�)����AD���ʵ��ƶ����ǰ嶥��P:
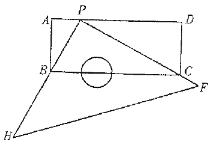
���ܷ�ʹ������ǰ���ֱ�DZ߷ֱ�ͨ����B���C?���������������ʱ AP �ij�������������˵��������
���ٴ��ƶ����ǰ�λ����ʹ���ǰ嶥��P��AD���ƶ���ֱ�DZ�PH ʼ��ͨ����B����һֱ�DZ�PF��DC���ӳ��߽��ڵ�Q����BC���ڵ�E���ܷ�ʹCE=2cm?���������������ʱAP�ij���������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���B=90����AB=16cm��BC=12cm��P��Q����ABC���ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊt�룮
��1������2�������PBQ�������
��2������Q�ڱ�BC���˶�ʱ�����������Ӻ���PQB���γɵ��������Σ�
��3������Q�ڱ�CA���˶�ʱ������ʹ��BCQ��Ϊ���������ε��˶�ʱ�䣮
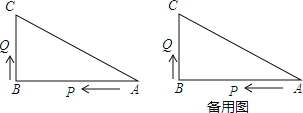
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С��һ�ҳ�������ǰ��ij�����Σ��ƻ��ڶ�����������Դ�����Լݳ��Ρ�
 [��
[��
����������Ϣ������������⣺
��1�����ʱ��Ϊ![]() Сʱ�����ü�˾�ij��������Ϊ
Сʱ�����ü�˾�ij��������Ϊ![]() Ԫ�������ҹ�˾�ij��������Ϊ
Ԫ�������ҹ�˾�ij��������Ϊ![]() Ԫ���ֱ����
Ԫ���ֱ����![]() ��
��![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������С�����㲢ѡ���ĸ����η������㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��y����һ��������T���涨��T��x��y����![]() ������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�����������㣬���磺T��0��1����
������a��b��Ϊ���㳣�����������ʽ�ұ���ͨ�����������㣬���磺T��0��1����![]() ��b����֪T��1��1����2.5��T��4����2����4��
��b����֪T��1��1����2.5��T��4����2����4��
��1����a��b��ֵ��
��2��������m�IJ���ʽ��![]() ǡ����2�������⣬��ʵ��P��ȡֵ��Χ��
ǡ����2�������⣬��ʵ��P��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊϲӭ�л���������![]() ���꣬ij��ѧ����������Ѱ��ɫ���������к�ɫ����Ϊ����������߳���·��������꼶��Ҫ���ľߵ깺�����ͼ����ֽ��С����ַ���ѧ����Ϊ����ߣ���֪ÿ����ֽ��
���꣬ij��ѧ����������Ѱ��ɫ���������к�ɫ����Ϊ����������߳���·��������꼶��Ҫ���ľߵ깺�����ͼ����ֽ��С����ַ���ѧ����Ϊ����ߣ���֪ÿ����ֽ��![]() �ţ�ÿ��С������
�ţ�ÿ��С������![]() �棬��ֽ��С�������������ס��������ľߵ�ı����ͬ��ÿ����ֽ�۸��ÿ��С����۸���
�棬��ֽ��С�������������ס��������ľߵ�ı����ͬ��ÿ����ֽ�۸��ÿ��С����۸���![]() Ԫ������
Ԫ������![]() ����ֽ��
����ֽ��![]() ��С����۸���ͬ��
��С����۸���ͬ��
(1)ˮÿ������ͼ����ֽ��ÿ��С����ļ۸���Ƕ���Ԫ��
(2)���������ֽ��С���ù�![]() ������ÿλ�μӻ��ѧ���ַ�����ͼ����ֽ
������ÿλ�μӻ��ѧ���ַ�����ͼ����ֽ![]() �ţ�С����
�ţ�С����![]() �棬ǡ��ȫ�����꣬���ʸ�У���꼶�ж�����ѧ����
�棬ǡ��ȫ�����꣬���ʸ�У���꼶�ж�����ѧ����
(3)��(2)�����£������ľߵ���Ż����£�
���ľߵ꣺ȫ����Ʒ���ﳬ��![]() Ԫ����
Ԫ����![]() Ԫ�IJ��ִ�����ۣ�
Ԫ�IJ��ִ�����ۣ�
���ľߵ꣺��ͬ��Ʒ������ʮ����һ��" ��
�������ļ��ľߵ깺��Ƚ��Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪij���в��ֵֽ�ʾ��ͼ���ı���ABCDΪ�����Σ���G�ڶԽ���BD�ϣ�GE��CD��GF��BC��AD��1 500 m��С�����ߵ�·��ΪB��A��G��E��С�����ߵ�·��ΪB��A��D��E��F.��С�����ߵ�·��Ϊ3 100 m����AG��GE��______m���ɴ˿ɵ�С�����ߵ�·��Ϊ_______m.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com