
ΓΨΧβΡΩΓΩΈΣœ≤”≠÷–ΜΣ»ΥΟώΙ≤ΚΆΙζ≥…ΝΔ![]() ÷ήΡξΘ§Ρ≥÷–―ßΫΪΨΌ––“‘ΓΑΉΖ―ΑΚλ…Ϊ–≈―ωΘ§¥Ϊ≥–Κλ…ΪΜυ“ρΓ±ΈΣ÷ςΧβΒΡΓΑ÷ΊΉΏ≥Λ’ς¬ΖΓ±ΜνΕ·Θ°ΤΏΡξΦΕ–η“Σ‘ΎΈΡΨΏΒξΙΚ¬ρΙζΤλΆΦΑΗΧυ÷ΫΚΆ–ΓΚλΤλΖ÷ΖΔΗχ―ß…ζΉςΈΣΜνΕ·ΒάΨΏΘ§“―÷ΣΟΩ¥ϋΧυ÷Ϋ”–
÷ήΡξΘ§Ρ≥÷–―ßΫΪΨΌ––“‘ΓΑΉΖ―ΑΚλ…Ϊ–≈―ωΘ§¥Ϊ≥–Κλ…ΪΜυ“ρΓ±ΈΣ÷ςΧβΒΡΓΑ÷ΊΉΏ≥Λ’ς¬ΖΓ±ΜνΕ·Θ°ΤΏΡξΦΕ–η“Σ‘ΎΈΡΨΏΒξΙΚ¬ρΙζΤλΆΦΑΗΧυ÷ΫΚΆ–ΓΚλΤλΖ÷ΖΔΗχ―ß…ζΉςΈΣΜνΕ·ΒάΨΏΘ§“―÷ΣΟΩ¥ϋΧυ÷Ϋ”–![]() ’≈Θ§ΟΩ¥ϋ–ΓΚλΤλ”–
’≈Θ§ΟΩ¥ϋ–ΓΚλΤλ”–![]() ΟφΘ§Χυ÷ΫΚΆ–ΓΚλΤλ–η’ϊ¥ϋΙΚ¬ρΘ°ΦΉΓΔ““ΝΫΦ“ΈΡΨΏΒξΒΡ±ξΦέœύΆ§Θ§ΟΩ¥ϋΧυ÷ΫΦέΗώ±»ΟΩ¥ϋ–ΓΚλΤλΦέΗώ…Ό
ΟφΘ§Χυ÷ΫΚΆ–ΓΚλΤλ–η’ϊ¥ϋΙΚ¬ρΘ°ΦΉΓΔ““ΝΫΦ“ΈΡΨΏΒξΒΡ±ξΦέœύΆ§Θ§ΟΩ¥ϋΧυ÷ΫΦέΗώ±»ΟΩ¥ϋ–ΓΚλΤλΦέΗώ…Ό![]() ‘ΣΘ§Εχ«“
‘ΣΘ§Εχ«“![]() ¥ϋΧυ÷Ϋ”κ
¥ϋΧυ÷Ϋ”κ![]() ¥ϋ–ΓΚλΤλΦέΗώœύΆ§Θ°
¥ϋ–ΓΚλΤλΦέΗώœύΆ§Θ°
(1)Υ°ΟΩ¥ϋΙζΤλΆΦΑΗΧυ÷ΫΚΆΟΩ¥ϋ–ΓΚλΤλΒΡΦέΗώΗς «Εύ…Ό‘ΣΘΩ
(2)»γΙϊΙΚ¬ρΧυ÷ΫΚΆ–ΓΚλ¬ΟΙ≤![]() ¥ϋΘ§ΗχΟΩΈΜ≤ΈΦ”ΜνΕ·ΒΡ―ß…ζΖ÷ΖΔΙζΤλΆΦΑΗΧυ÷Ϋ
¥ϋΘ§ΗχΟΩΈΜ≤ΈΦ”ΜνΕ·ΒΡ―ß…ζΖ÷ΖΔΙζΤλΆΦΑΗΧυ÷Ϋ![]() ’≈Θ§–ΓΚλΤλ
’≈Θ§–ΓΚλΤλ![]() ΟφΘ§«ΓΚΟ»Ϊ≤ΩΖ÷ΆξΘ§«κΈ ΗΟ–ΘΤΏΡξΦΕ”–Εύ…ΌΟϊ―ß…ζΘΩ
ΟφΘ§«ΓΚΟ»Ϊ≤ΩΖ÷ΆξΘ§«κΈ ΗΟ–ΘΤΏΡξΦΕ”–Εύ…ΌΟϊ―ß…ζΘΩ
(3)‘Ύ(2)ΧθΦΰœ¬Θ§ΝΫΦ“ΈΡΨΏΒξΒΡ”≈Μί»γœ¬ΘΚ
ΦΉΈΡΨΏΒξΘΚ»Ϊ≥Γ…ΧΤΖΙΚΈο≥§Ιΐ![]() ‘ΣΚσΘ§≥§≥ω
‘ΣΚσΘ§≥§≥ω![]() ‘ΣΒΡ≤ΩΖ÷¥ρΑΥΈε’έΘΜ
‘ΣΒΡ≤ΩΖ÷¥ρΑΥΈε’έΘΜ
““ΈΡΨΏΒξΘΚœύΆ§…ΧΤΖΘ§ΓΑ¬ρ °Φΰ‘υ“ΜΦΰ" Θ°
«κΈ ‘ΎΡΡΦ“ΈΡΨΏΒξΙΚ¬ρ±»Ϋœ”≈ΜίΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΩ¥ϋΙζΤλΆΦΑΗΧυ÷ΫΒΡΦέΗώ «![]() ‘ΣΘ§ΟΩ¥ϋ–ΓΚλΤλΒΡΦέΗώ «
‘ΣΘ§ΟΩ¥ϋ–ΓΚλΤλΒΡΦέΗώ «![]() ‘ΣΘΜΘ®2Θ©ΤΏΡξΦΕ”–
‘ΣΘΜΘ®2Θ©ΤΏΡξΦΕ”–![]() Οϊ―ß…ζΘΜΘ®3Θ©‘ΎΦΉΓΔ““ΝΫΦ“ΈΡΨΏΒξΙΚ¬ρΆ§―υ”≈ΜίΘ°
Οϊ―ß…ζΘΜΘ®3Θ©‘ΎΦΉΓΔ““ΝΫΦ“ΈΡΨΏΒξΙΚ¬ρΆ§―υ”≈ΜίΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηΟΩ¥ϋΧυ÷Ϋ![]() ‘ΣΘ§ΟΩ¥ϋΚλΤλ
‘ΣΘ§ΟΩ¥ϋΚλΤλ![]() Θ§Ν–≥ωΖΫ≥ΧΩ…ΒΟ≥ω¥πΑΗΘΜ
Θ§Ν–≥ωΖΫ≥ΧΩ…ΒΟ≥ω¥πΑΗΘΜ
Θ®2Θ©…ηΙΚ¬ρΧυ÷Ϋ![]() ¥ϋΘ§ΙΚ¬ρ–ΓΚλΤλ
¥ϋΘ§ΙΚ¬ρ–ΓΚλΤλ![]() ¥ϋΘ§Ν–≥ωΖΫ≥ΧΦ¥Ω…«σΫβ¥πΑΗΘΜ
¥ϋΘ§Ν–≥ωΖΫ≥ΧΦ¥Ω…«σΫβ¥πΑΗΘΜ
Θ®3Θ©Ζ÷±πΦΤΥψ≥ωΝΫΦ“ΈΡΨΏΒξ”ΠΗΕΫπΕν‘ΌΫχ––±»ΫœΦ¥Ω…Θ°
ΫβΘΚ (1) …ηΟΩ¥ϋΧυ÷Ϋ![]() ‘ΣΘ§ΟΩ¥ϋΚλΤλ
‘ΣΘ§ΟΩ¥ϋΚλΤλ![]() ‘ΣΘ§ΗυΨίΧβ“βΒΟΘ§
‘ΣΘ§ΗυΨίΧβ“βΒΟΘ§
![]()
ΫβΒΟΘΚ![]()
![]() (‘Σ)Θ°
(‘Σ)Θ°
¥πΘΚΟΩ¥ϋΙζΤλΆΦΑΗΧυ÷ΫΒΡΦέΗώ «![]() ‘ΣΘ§ΟΩ¥ϋ–ΓΚλΤλΒΡΦέΗώ «
‘ΣΘ§ΟΩ¥ϋ–ΓΚλΤλΒΡΦέΗώ «![]() ‘ΣΘ°
‘ΣΘ°
(2)…ηΙΚ¬ρΧυ÷Ϋ![]() ¥ϋΘ§ΙΚ¬ρ–ΓΚλΤλ
¥ϋΘ§ΙΚ¬ρ–ΓΚλΤλ![]() ¥ϋΘ§ΗυΨίΧβ“βΒΟΘ§ Θ°
¥ϋΘ§ΗυΨίΧβ“βΒΟΘ§ Θ°
![]()
ΫβΒΟΘΚ![]()
![]() ΤΏΡξΦΕΒΡ»Υ ΐΈΣΘΚ
ΤΏΡξΦΕΒΡ»Υ ΐΈΣΘΚ ![]() (Οϊ)
(Οϊ)
¥πΘΚΤΏΡξΦΕ”–![]() Οϊ―ß…ζΘΚ
Οϊ―ß…ζΘΚ
(3)”…(2)÷ΣΙΚ¬ρΧυ÷Ϋ![]() ¥ϋΘ§ΙΚ¬ρ–ΓΚλΤλ
¥ϋΘ§ΙΚ¬ρ–ΓΚλΤλ![]() ¥ϋΘ§
¥ϋΘ§
![]() Χυ÷ΫΟΩ¥ϋ
Χυ÷ΫΟΩ¥ϋ![]() ‘ΣΘ§ΚλΤλΟΩ¥ϋ
‘ΣΘ§ΚλΤλΟΩ¥ϋ![]() ‘ΣΘ§
‘ΣΘ§
![]() »Ϊ≤ΩΫπΕνΈΣΘΚ
»Ϊ≤ΩΫπΕνΈΣΘΚ ![]() (‘Σ)Θ§
(‘Σ)Θ§
‘ΎΦΉΈΡΨΏΒξ”ΠΗΕΫπΕνΈΣΘΚ![]() (‘Σ)ΘΜ
(‘Σ)ΘΜ
‘Ύ““ΈΡΨΏΒξ”ΠΗΕΫπΕνΈΣΘΚ ![]() (‘Σ)Θ§
(‘Σ)Θ§
¥πΘΚ‘ΎΦΉΓΔ““ΝΫΦ“ΈΡΨΏΒξΙΚ¬ρΆ§―υ”≈ΜίΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣA(0Θ§a)Θ§B(bΘ§0)Θ§C(bΘ§4)»ΐΒψΘ§Τδ÷–aΘ§b¬ζΉψΙΊœΒ ΫaΘΫ![]() ΘΪ2.»τ‘ΎΒΎΕΰœσœόΡΎ”–“ΜΒψP(mΘ§1)Θ§ ΙΥΡ±Ώ–ΈABOPΒΡΟφΜΐ”κ»ΐΫ«–ΈABCΒΡΟφΜΐœύΒ»Θ§‘ρΒψPΒΡΉχ±ξΈΣ(ΓΓΓΓ)
ΘΪ2.»τ‘ΎΒΎΕΰœσœόΡΎ”–“ΜΒψP(mΘ§1)Θ§ ΙΥΡ±Ώ–ΈABOPΒΡΟφΜΐ”κ»ΐΫ«–ΈABCΒΡΟφΜΐœύΒ»Θ§‘ρΒψPΒΡΉχ±ξΈΣ(ΓΓΓΓ)
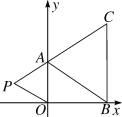
A. (Θ≠3Θ§1) B. (Θ≠2Θ§1) C. (Θ≠4Θ§1) D. (Θ≠2.5Θ§1)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ABΓΈCDΓΈx÷αΘ§BCΓΈDEΓΈy÷αΘ§«“AB=CD=4cmΘ§OA=5cmΘ§DE=2cmΘ§Ε·ΒψP¥”ΒψA≥ωΖΔΘ§―ΊAΓζBΓζC¬ΖœΏ‘ΥΕ·ΒΫΒψCΆΘ÷ΙΘΜΕ·ΒψQ¥”ΒψO≥ωΖΔΘ§―ΊOΓζEΓζDΓζC¬ΖœΏ‘ΥΕ·ΒΫΒψCΆΘ÷ΙΘΜ»τPΓΔQΝΫΒψΆ§ ±≥ωΖΔΘ§«“ΒψPΒΡ‘ΥΕ·ΥΌΕ»ΈΣ1cm/sΘ§ΒψQΒΡ‘ΥΕ·ΥΌΕ»ΈΣ2cm/sΘ°
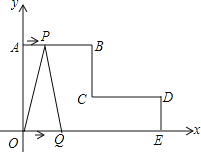
Θ®1Θ©÷±Ϋ”–¥≥ωBΓΔCΓΔD»ΐΗωΒψΒΡΉχ±ξΘΜ
Θ®2Θ©Β±PΓΔQΝΫΒψ≥ωΖΔ![]() s ±Θ§ ‘«σΓςPQCΒΡΟφΜΐΘΜ
s ±Θ§ ‘«σΓςPQCΒΡΟφΜΐΘΜ
Θ®3Θ©…ηΝΫΒψ‘ΥΕ·ΒΡ ±ΦδΈΣt sΘ§”ΟtΒΡ ΫΉ”±μ Ψ‘ΥΕ·Ιΐ≥Χ÷–ΓςOPQΒΡΟφΜΐSΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψO «ΓςABCΡΎ“ΜΒψΘ§Ν§Ϋ”OBΘ§OCΘ§≤ΔΫΪABΘ§OBΘ§OCΘ§ACΒΡ÷–ΒψDΘ§EΘ§FΘ§G“ά¥ΈΝ§Ϋ”ΒΟΒΫΥΡ±Ώ–ΈDEFGΘ°
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈDEFG «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©»τOBΓΆOCΘ§ΓœEOMΚΆΓœOCBΜΞ”ύΘ§OMΘΫ3Θ§«σDGΒΡ≥ΛΕ»Θ°
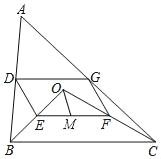
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΈΣΝΥΦλ―ιΫΧ “άοΒΡΨΊ–ΈΟ≈Ωρ «ΖώΚœΗώΘ§Ρ≥ΑύΒΡΥΡΗω―ßœΑ–ΓΉι”Ο»ΐΫ«ΑεΚΆœΗ…ΰΖ÷±π≤βΒΟ»γœ¬ΫαΙϊΘ§Τδ÷–≤ΜΡή≈–Ε®Ο≈Ωρ «ΖώΚœΗώΒΡ «Θ® Θ©

A. AB=CDΘ§AD=BCΘ§AC=BD B. AC=BDΘ§ΓœB=ΓœC=90Γψ C. AB=CDΘ§ΓœB=ΓœC=90Γψ D. AB=CDΘ§AC=BD
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣAΘ§BΝΫΒΊœύΨύ80kmΘ§ΦΉΘ§““ΝΫ»Υ―ΊΆ§“ΜΧθΙΪ¬Ζ¥”AΒΊ≥ωΖΔΒΫBΒΊΘ§““ΤοΉ‘––≥ΒΘ§ΦΉΤοΡΠΆ–≥ΒΘ°ΆΦ÷–DEΘ§OCΖ÷±π±μ ΨΦΉΘ§““άκΩΣAΒΊΒΡ¬Ζ≥ΧsΘ®kmΘ©”κ ±ΦδtΘ®hΘ©ΒΡΚ· ΐΙΊœΒΘ§ΗυΨίΆΦœσΒΟ≥ωΒΡœ¬Ν––≈œΔ¥μΈσΒΡ «Θ® Θ© 
A.““ΒΫ¥οBΒΊ ±ΦΉΨύAΒΊ120km
B.““≥ωΖΔ1.8–Γ ±±ΜΦΉΉΖ…œ
C.ΦΉΘ§““œύΨύ20km ±Θ§tΈΣ2.4h
D.ΦΉΒΡΥΌΕ» «““ΒΡΥΌΕ»ΒΡ ![]() ±Ε
±Ε
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γ“ΣΨ≠”Σ“Μ÷÷–¬…œ –ΒΡΈΡΨΏΘ§ΫχΦέΈΣ20‘Σ/ΦΰΘ§ ‘”ΣœζΫΉΕΈΖΔœ÷ΘΚΒ±œζ έΒΞΦέ «25‘Σ ±Θ§ΟΩΧλΒΡœζ έΝΩΈΣ250ΦΰΘ§œζ έΒΞΦέΟΩ…œ’«1‘ΣΘ§ΟΩΧλΒΡœζ έΝΩΨΆΦθ…Ό10Φΰ
Θ®1Θ©–¥≥ω…Χ≥Γœζ έ’β÷÷ΈΡΨΏΘ§ΟΩΧλΥυΒΟΒΡœζ έάϊ»σwΘ®‘ΣΘ©”κœζ έΒΞΦέxΘ®‘ΣΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©«σœζ έΒΞΦέΈΣΕύ…Ό‘Σ ±Θ§ΗΟΈΡΨΏΟΩΧλΒΡœζ έάϊ»σΉν¥σΘΜ
Θ®3Θ©…Χ≥ΓΒΡ”Σœζ≤ΩΫαΚœ…œ ω«ιΩωΘ§Χα≥ωΝΥAΓΔBΝΫ÷÷”ΣœζΖΫΑΗΘΚ
ΖΫΑΗAΘΚΗΟΈΡΨΏΒΡœζ έΒΞΦέΗΏ”ΎΫχΦέ«“≤Μ≥§Ιΐ30‘ΣΘΜ
ΖΫΑΗBΘΚΟΩΧλœζ έΝΩ≤Μ…Ό”Ύ10ΦΰΘ§«“ΟΩΦΰΈΡΨΏΒΡάϊ»σ÷Ν…ΌΈΣ25‘ΣΘ°«κ±»ΫœΡΡ÷÷ΖΫΑΗΒΡΉν¥σάϊ»σΗϋΗΏΘ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡ–Γ’ΐΖΫ–ΈΉι≥…ΒΡΆχΗώ÷–Θ§
ΗωΒΞΈΜ≥ΛΕ»ΒΡ–Γ’ΐΖΫ–ΈΉι≥…ΒΡΆχΗώ÷–Θ§![]() ΓΔ’ΐΖΫ–Έ
ΓΔ’ΐΖΫ–Έ![]() ΓΔ’ΐΖΫ–Έ
ΓΔ’ΐΖΫ–Έ![]() ΒΡΕΞΒψΨυ‘ΎΗώΒψ…œΘ°
ΒΡΕΞΒψΨυ‘ΎΗώΒψ…œΘ°
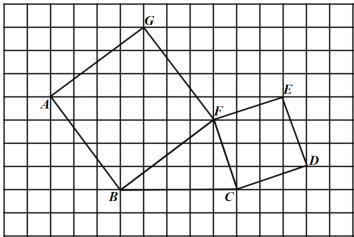
Θ®1Θ©“‘ΗώΒψΈΣ‘≠ΒψΘ§Ϋ®ΝΔΚœ ΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§ ΙΒΟ![]() ΓΔ
ΓΔ![]() Ήχ±ξΖ÷±πΈΣ
Ήχ±ξΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§‘ρΒψ
Θ§‘ρΒψ![]() ΒΡΉχ±ξΈΣ______Θ§Βψ
ΒΡΉχ±ξΈΣ______Θ§Βψ![]() ΒΡΉχ±ξΈΣ_______ΘΜ
ΒΡΉχ±ξΈΣ_______ΘΜ
Θ®2Θ©άϊ”ΟΟφΜΐΦΤΥψœΏΕΈ![]() ________ΘΜ
________ΘΜ
Θ®3Θ©Βψ![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œ“ΜΕ·ΒψΘ§«σ
…œ“ΜΕ·ΒψΘ§«σ![]() ΒΡΉν–Γ÷ΒΘ°
ΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§≈ΉΈοœΏy=ax2+bx+4 ”κx÷αΫΜ”ΎΒψAΘ®©¹3Θ§0Θ©ΚΆBΘ®2Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§»τΒψDΈΣCBΒΡ÷–ΒψΘ§ΫΪœΏΕΈDB»ΤΒψD–ΐΉΣΘ§ΒψBΒΡΕ‘”ΠΒψΈΣΒψGΘ§Β±ΒψG«ΓΚΟ¬δ‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ ±Θ§«σΒψGΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦ2Θ§»τΒψDΈΣ÷±œΏBCΜρ÷±œΏAC…œΒΡ“ΜΒψΘ§EΈΣx÷α…œ“ΜΕ·ΒψΘ§≈ΉΈοœΏ
y=ax2+bx+4Ε‘≥Τ÷α…œ «Ζώ¥φ‘ΎΒψFΘ§ Ι“‘BΘ§DΘ§FΘ§EΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΈΣΝβ–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψFΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com