
【题目】已知,抛物线y=ax2+bx+4 与x轴交于点A(﹣3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线
y=ax2+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
【答案】
(1)解:∵抛物线y=ax2+bx+4 与x轴交于点A(﹣3,0)和B(2,0),
∴ ![]() ,解得
,解得  ,
,
∴抛物线解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+4
x+4
(2)解:由(1)可知抛物线的对称轴为x=﹣ ![]() .
.
∴可设点G的坐标为(﹣ ![]() ,y),
,y),
∵点D是BC的中点,
∴点D的坐标为(1,2),
在Rt△OBC中,BC= ![]() =2
=2 ![]() .
.
∴DB= ![]() BC=
BC= ![]() ,
,
由旋转的性质可知,DG=DB,
∴(﹣ ![]() ﹣1)2+(y﹣2)2=5,解得:y=2+
﹣1)2+(y﹣2)2=5,解得:y=2+ ![]() 或y=2﹣
或y=2﹣ ![]() ,
,
∴点G的坐标为(﹣ ![]() ,2+
,2+ ![]() )或(﹣
)或(﹣ ![]() ,2﹣
,2﹣ ![]() )
)
(3)解:①当BE为对角线时,因为菱形的对角线互相垂直平分,所以此时D即为对称轴与AC的交点,F为点D关于x轴的对称点,
设直线AC解析式为y=kx+b,
∵C(0,4),A(﹣3,0)
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AC解析式为y= ![]() x+4,
x+4,
∴当 ![]() 时,
时, ![]() ,
,
∴D ![]() ,
,
∴F ![]() ;
;
②当BE为菱形的边时,有DF∥BE
I)当点D在直线BC上时,可求得直线BC解析式为y=﹣2x+4,
设D(a,﹣2a+4),则点F ![]() ,
,
∵四边形BDFE是菱形,
∴FD=DB,
∴ ![]() ,解得
,解得 ![]() ,
, ![]() ,
,
∴F ![]() 或
或 ![]() ;
;
II)当点D在直线AC上时,
设D ![]() ,则点F
,则点F ![]() ,
,
∵四边形BFDE是菱形,
∴FD=FB,
∴(a+ ![]() )2=(2+
)2=(2+ ![]() )2+(
)2+( ![]() a+4)2,解得:a1=﹣3(舍去),
a+4)2,解得:a1=﹣3(舍去), ![]() ,
,
∴F ![]() ,
,
综上所述,点F的坐标分别为 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]()
【解析】(1)把A、B两点的坐标代入抛物线解析式可求得a、b的值,可求得抛物线解析式;(2)可设出G点坐标,利用旋转的性质可求得DG=DB,从而可列出方程,可求得G点坐标;(3)分BE为对角线和BE为边两种情况,①当BE为对角线时,则可知BE⊥DF,可知D为对称轴与直线AC的交点,F为D点关于x轴的对称点,可先求得直线AC的解析式,可求得D点坐标,则容易求得F点坐标;②当BE为边时,可利用直线BC或直线AC的解析式设出点D的坐标,从而可表示出F点的坐标,再利用菱形的性质可列出方程,从而可求得F点的坐标.


科目:初中数学 来源: 题型:
【题目】为喜迎中华人民共和国成立![]() 周年,某中学将举行以“追寻红色信仰,传承红色基因”为主题的“重走长征路”活动.七年级需要在文具店购买国旗图案贴纸和小红旗分发给学生作为活动道具,已知每袋贴纸有
周年,某中学将举行以“追寻红色信仰,传承红色基因”为主题的“重走长征路”活动.七年级需要在文具店购买国旗图案贴纸和小红旗分发给学生作为活动道具,已知每袋贴纸有![]() 张,每袋小红旗有
张,每袋小红旗有![]() 面,贴纸和小红旗需整袋购买.甲、乙两家文具店的标价相同,每袋贴纸价格比每袋小红旗价格少
面,贴纸和小红旗需整袋购买.甲、乙两家文具店的标价相同,每袋贴纸价格比每袋小红旗价格少![]() 元,而且
元,而且![]() 袋贴纸与
袋贴纸与![]() 袋小红旗价格相同.
袋小红旗价格相同.
(1)水每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果购买贴纸和小红旅共![]() 袋,给每位参加活动的学生分发国旗图案贴纸
袋,给每位参加活动的学生分发国旗图案贴纸![]() 张,小红旗
张,小红旗![]() 面,恰好全部分完,请问该校七年级有多少名学生?
面,恰好全部分完,请问该校七年级有多少名学生?
(3)在(2)条件下,两家文具店的优惠如下:
甲文具店:全场商品购物超过![]() 元后,超出
元后,超出![]() 元的部分打八五折;
元的部分打八五折;
乙文具店:相同商品,“买十件赠一件" .
请问在哪家文具店购买比较优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则AG+GE=______m,由此可得小聪行走的路程为_______m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB= ![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1: ![]() (i为DF与FC的比值),则背水坡CD的坡长为米.
(i为DF与FC的比值),则背水坡CD的坡长为米.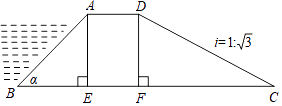
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.若AE=a,AB=b,BF=c,请写出a,b,c之间的一个等量关系为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在直角坐标系内的位置如图所示
(1)分别写出点A,C的坐标:A: ,C: ;
(2)△ABC的周长为 ,面积为 ;
(3)请在这个坐标系内画出△A1B1C1与△ABC关于x轴对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4. 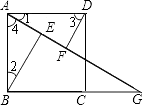
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
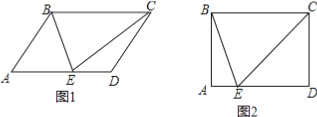
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com