
【题目】如图,把矩形ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.若AE=a,AB=b,BF=c,请写出a,b,c之间的一个等量关系为__________.

【答案】c2=a2+b2
【解析】
连接BE,由四边形ABCD为矩形可以得出AD∥BC,就有∠DEF=∠BFE,根据轴对称就可以得出△A'B'E≌△ABE,△B'EF≌△BEF,就可以得出B'E=BE,B'F=BF,∠B'FE=∠BFE,就可以得出∠B'FE=∠B'EF,就有B'E=B'F,就有B'E=BF,由勾股定理即可得出结论.
c2=a2+b2.理由:连接BE.
∵四边形ABCD是矩形,∴∠A=∠B=90°.AD∥BC,∴∠DEF=∠BFE.
∵△A'B'E与△ABE,△B'EF与△BEF关于EF成轴对称,∴△A'B'E≌△ABE,△B'EF≌△BEF,∴B'E=BE,B'F=BF,AE=A'E,A'B'=AB,∠B'FE=∠BFE,∠A=∠A'=90°,∴∠B'EF=∠B'FE,∴B'E=B'F,∴B'E=BF.
∵AE=a,AB=b,BF=c,∴A'E=a,A'B'=b,B'E=c.
∵∠A'=90°,∴c2=a2+b2.


科目:初中数学 来源: 题型:
【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )

A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为2,a2+1,则点P所在的象限是____;以方程组![]() 的解为坐标的点x,y在平面直角坐标系中的位置是__________;在平面直角坐标系中,如果mn>0,请写出点m,|n|可能在的所有象限:____________.
的解为坐标的点x,y在平面直角坐标系中的位置是__________;在平面直角坐标系中,如果mn>0,请写出点m,|n|可能在的所有象限:____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第1个等式:1-![]() =
=![]() ×
×![]()
第2个等式:(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第3个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第4个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
第5个等式:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ×
×![]()
······
(1) 写出第6个等式;
(2) 写出第n个等式(用含n的等式表示),并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+bx+4 与x轴交于点A(﹣3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线
y=ax2+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC为一个电子跳蚤游戏盘,其中AB=8,AC=9,BC=10.如果电子跳蚤开始时在BC边上的点P0处,BP0=4,第一步跳蚤从点P0处跳到AC边上的点P1处,且CP1=CP0;第二步跳蚤从点P1处跳到AB边上的点P2处,且AP1=AP2;第三步跳蚤从点P2处跳回到BC边上的点P3处,且BP3=BP2……若跳蚤按上述规则跳下去,第n次的落点为Pn,则点P3与点P2019之间的距离为( )
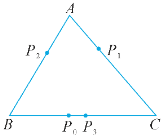
A. 0 B. 1 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
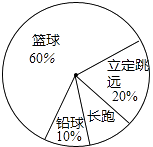
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com