
【题目】在![]() 中,
中, ![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折线,将
为折线,将![]() 翻折,设所得的
翻折,设所得的![]() 与梯形
与梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
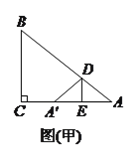
(![]() )如图(甲),若
)如图(甲),若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的值为__________.
的值为__________.
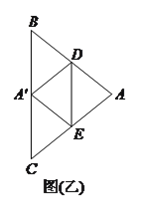
(![]() )如图(乙),若
)如图(乙),若![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,则
中点,则![]() 的值为__________.
的值为__________.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
①求![]() 与
与![]() 的函数解析式.
的函数解析式.
②![]() 是否有最大值,若有,求出
是否有最大值,若有,求出![]() 的最大值;若没有,请说明理由.
的最大值;若没有,请说明理由.
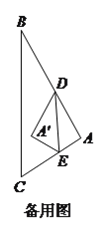
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①
;(3)①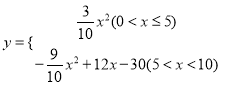 ;②当
;②当![]() 时,
时, ![]() 值最大,最大值为
值最大,最大值为![]() .
.
【解析】试题分析:(1)本题需先根据已知条件得出AC的长,再根据DE∥BC得出△ADE∽△ABC,再根据面积之比等于相似比的平方即可求出结果.
(2)本题需先根据已知条件得出BC边上的高的值和S△ABC的值,再根据D为AB中点和DE∥BC,即可得出△ADE∽△ABC,最后根据面积之比等于相似比的平方即可求出结果;
(3)本题需先作AH⊥BC于点H,根据已知条件得出AH和S△ABC的值,再分两种情况0<x≤5时和当5<x<10进行讨论,分别求出![]() 和
和![]() 的值,即可求出y的最大值.
的值,即可求出y的最大值.
解:(![]() )∵
)∵![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴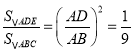 ,∴
,∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() 边上的高为
边上的高为![]() ,∴
,∴![]() ,∵
,∵![]() 为
为![]() 的中点,
的中点, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴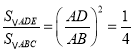 ,∴
,∴![]() ,∴
,∴![]() .
.
(![]() )如图a,作
)如图a,作![]() 于点
于点![]() ,在
,在![]() 中,∵
中,∵![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,当
,当![]() 落在
落在![]() 上时,
上时, ![]() 为
为![]() 的中点:
的中点:

即![]() 故分以下两种情况讨论:
故分以下两种情况讨论:
①当![]() 时,如图b,∵
时,如图b,∵![]() ,∴
,∴![]() ,∴
,∴ ,∴
,∴![]() ,即
,即![]() ,∴当
,∴当![]() 时,
时, ![]() .
.
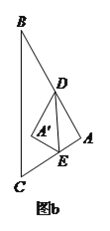
②当![]() 时,如图c,设
时,如图c,设![]() ,
, ![]() 分别交
分别交![]() 于
于![]() ,
, ![]() ,由折叠可知,
,由折叠可知, ![]() ,∴
,∴![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,由①同理得
,由①同理得![]() ,又
,又![]() ,∴
,∴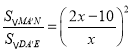 ,∴
,∴![]() ,∴
,∴![]()
![]()
∵![]() ,且当
,且当![]() 时满足
时满足![]() ,∴
,∴![]() 。
。
∴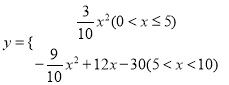
当![]() 时,
时, ![]() 值最大,最大值为
值最大,最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F为CE的中点,连接DF.给出以下五个结论:①BD=DC;②AD=2DF;③ ![]() ;④DF是⊙O的切线.其中正确结论的个数是:( )
;④DF是⊙O的切线.其中正确结论的个数是:( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
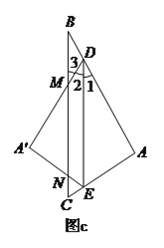
【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知菱形![]() 的边长为12,
的边长为12,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
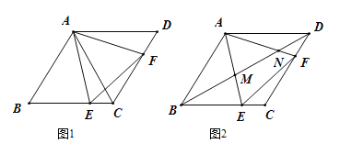
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,各超市购物市民络绎不绝,呈现浓浓节日气氛.“百姓超市”用320元购进一批葡萄,上市后很快脱销,该超市又用680元购进第二批葡萄,所购数量是第一批购进数量的2倍,但进价每千克多了0.2元.
(1)该超市第一批购进这种葡萄多少千克?
(2)如果这两批购进的葡萄售价相同,且全部售完后利润率不低于20%,那么每千克葡萄的售价应该至少定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
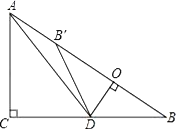
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,若点P是⊙O外的一点,线段PO交⊙O于点A,则PA长是点P与⊙O上各点之间的最短距离.
证明:延长PO交⊙O于点B,显然PB>PA.
如图2,在⊙O上任取一点C(与点A,B不重合),连结PC,OC.
∵PO<PC+OC,
且PO=PA+OA,OA=OC,
∴PA<PC
∴PA 长是点P与⊙O上各点之间的最短距离.
由此可以得到真命题:圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差.请用上述真命题解决下列问题.
(1)如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是![]() 上的一个动点,连接AP,则AP长的最小值是 .
上的一个动点,连接AP,则AP长的最小值是 .
(2)如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,①求线段A’M的长度; ②求线段A′C长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并回答下列问题:
在平面直角坐标系 xOy 中, 点 P x, y 经过 f 变换得到点 P x, y , 变换记作f x, y x, y, 其中![]() ,例如,当a=1,b=1时,则点(-1,2)经过f变换,
,例如,当a=1,b=1时,则点(-1,2)经过f变换,![]() ,即
,即![]() .
.
(1)当 a 1, b 1时,则 f 0, 1 .
(2)若 f 2,3 4, 2 ,求 a 和b 的值.
(3)若象限内点 P x, y 的横纵坐标满足 y 3x ,点 P 经过 f 变换得到点 P x, y,若点 P 与点 P重合,求 a 和b 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com