
【题目】阅读材料并回答下列问题:
在平面直角坐标系 xOy 中, 点 P x, y 经过 f 变换得到点 P x, y , 变换记作f x, y x, y, 其中![]() ,例如,当a=1,b=1时,则点(-1,2)经过f变换,
,例如,当a=1,b=1时,则点(-1,2)经过f变换,![]() ,即
,即![]() .
.
(1)当 a 1, b 1时,则 f 0, 1 .
(2)若 f 2,3 4, 2 ,求 a 和b 的值.
(3)若象限内点 P x, y 的横纵坐标满足 y 3x ,点 P 经过 f 变换得到点 P x, y,若点 P 与点 P重合,求 a 和b 的值.
【答案】(1)(1,1);(2)![]() ;(3)
;(3)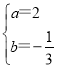 .
.
【解析】
(1)将a=1,b=1,f(0,1)代入![]() ,可求x′,y′的值,从而求解;
,可求x′,y′的值,从而求解;
(2)将f(2,3)=(4,2)代入![]() ,可得关于a,b的二元一次方程组,解方程组即可求解;
,可得关于a,b的二元一次方程组,解方程组即可求解;
(3)由点P(x,y)经过变换f得到的对应点P'(x',y')与点P重合,点P(x,y)在直线y=3x上,可得f(x,y)=(x,y),f(x,3x)=(x,3x),得到关于a,b的二元一次方程组,解方程组即可求解.
解:(1)当a=1,b=1时,
x′=1×0+(1)×(1)=1,y′=1×0(1)×(1)=1,
则f(0,1)=(1,1);
故答案为:(1,1);
(2)∵f(2,3)=(4,2),
∴![]() ,
,
解得![]() ;
;
(3)∵点P(x,y)经过变换f得到的对应点P'(x',y')与点P重合,
∴f(x,y)=(x,y).
∵点P(x,y)在直线y=3x上,
∴f(x,3x)=(x,3x).
∴![]() ,
,
即![]() ,
,
∵x为任意的实数,
∴![]() ,
,
解得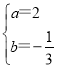 .
.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折线,将
为折线,将![]() 翻折,设所得的
翻折,设所得的![]() 与梯形
与梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
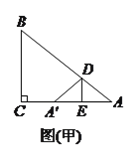
(![]() )如图(甲),若
)如图(甲),若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的值为__________.
的值为__________.
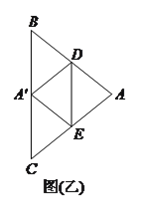
(![]() )如图(乙),若
)如图(乙),若![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,则
中点,则![]() 的值为__________.
的值为__________.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
①求![]() 与
与![]() 的函数解析式.
的函数解析式.
②![]() 是否有最大值,若有,求出
是否有最大值,若有,求出![]() 的最大值;若没有,请说明理由.
的最大值;若没有,请说明理由.
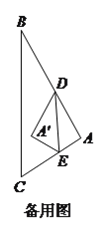
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“和谐数对”,记为(a,b).
成立的一对数a,b为“和谐数对”,记为(a,b).
(1)若(3,x)是“和谐数对”,求x的值;
(2)若(m,n)是“和谐数对”,求代数式![]() 的值;
的值;
(3)有一个“和谐数对”(a,b),满足a-b=1,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
①ac![]()
②a﹣b+c>0;
③当![]() 时,y随x的增大而增大
时,y随x的增大而增大
若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1
,y2)是抛物线上的两点,则y1![]() y2;
y2;
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
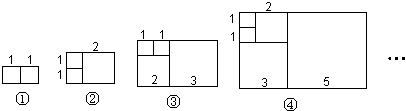
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ABCD中,AB 6cm ,BC 12cm ,B 30,点P 在 BC 上由点B向点C 出发,速度为每秒2cm;点Q 在边AD上,同时由点 D 向点 A 运动,速度为每秒1cm ,当点 P 运动到点C时,P 、Q 同时停止运动,连接 PQ,设运动时间为t秒.
(1)当t为何值时四边形 ABPQ 为平行四边形?
(2)当t为何值时,四边形 ABPQ 的面积是四边形 ABCD 的面积的四分之三?
(3)连接 AP ,是否存在某一时刻t,使ABP 为等腰三角形?并求出此刻t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com