练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】能判定四边形是平行四边形的是（ ）

    A.AB∥CD，B. AB∥CD，

    C.，D.，

    【答案】B

    【解析】

    平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的5种判定定理逐一验证即可．

    解：如下图，

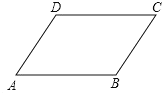
    A．根据一组对边平行，另一组对边相等不能判定四边形ABCD是平行四边形，故该选项错误；

    B．∵AB∥CD，

    ∴∠B+∠C=180°，

    ∵∠B=∠D，

    ∴∠C+∠D=180°，

    ∴AD∥BC，

    ∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)，故该选项正确；

    C．根据平行四边形的判定定理，该选项无法判断四边形是平行四边形，故该选项错误；

    D．根据平行四边形的判定定理，该选项无法判断四边形是平行四边形，故该选项错误．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料：如图1，若点P是⊙O外的一点，线段PO交⊙O于点A，则PA长是点P与⊙O上各点之间的最短距离．

    证明：延长PO交⊙O于点B，显然PB＞PA．

    如图2，在⊙O上任取一点C（与点A，B不重合），连结PC，OC．

    ∵PO＜PC+OC，

    且PO=PA+OA，OA=OC，

    ∴PA＜PC

    ∴PA 长是点P与⊙O上各点之间的最短距离．

    由此可以得到真命题：圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差．请用上述真命题解决下列问题．

    （1）如图3，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是 上的一个动点，连接AP，则AP长的最小值是　 　．

    （2）如图4，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，①求线段A’M的长度； ②求线段A′C长的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料并回答下列问题：

    在平面直角坐标系 xOy 中， 点 P x, y 经过 f 变换得到点 P x, y ， 变换记作f x, y x, y， 其中，例如，当a=1，b=1时，则点（-1，2）经过f变换，，即.

    （1）当 a 1， b 1时，则 f 0, 1 .

    （2）若 f 2,3 4, 2 ，求 a 和b 的值.

    （3）若象限内点 P x, y 的横纵坐标满足 y 3x ，点 P 经过 f 变换得到点 P x, y，若点 P 与点 P重合，求 a 和b 的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

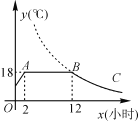
    【题目】我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种．如图是某天恒温系统从开启到关闭及关闭后，大棚内温度y(℃)随时间x(小时)变化的函数图象，其中BC段是双曲线y=的一部分．请根据图中信息解答下列问题：

    (1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时？

    (2)求k的值；

    (3)当x＝16时，大棚内的温度约为多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形纸片ABCD中，AB=4，将纸片折叠，使顶点B落在边AD上的点为E，折痕的一端G点在BC上（BG＜GC），另一端F落在矩形的边上，BG=5．

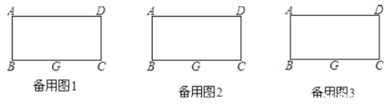
    （1）请你在备用图中画出满足条件的图形；

    （2）求出AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．

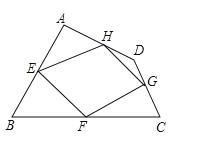
    （1）四边形EFGH的形状是什么，并证明你的结论．

    （2）当四边形ABCD的对角线满足什么条件时，四边形EFGH是矩形；并利用你给的条件加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点为角平分线交点， ，，，将平移使其顶点与重合，则图中阴影部分的周长为( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

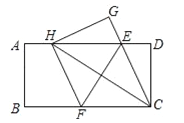
    【题目】如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：

    ①四边形CFHE是菱形；②线段BF的取值范围为3≤BF≤4；

    ③EC平分∠DCH；④当点H与点A重合时，EF=．

    以上结论中，你认为正确的有______．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC绕点A按逆时针方向旋转120°得到△AB'C'（点B的对应点是点B'，点C的对应点是点C'），连接BB'，若AC'∥BB'，则∠C'AB'的度数为（ ）

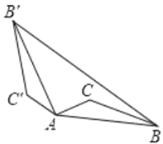
    A.20°B.30°C.40°D.50°

    查看答案和解析>>

    同步练习册答案