
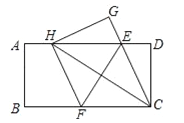
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②线段BF的取值范围为3≤BF≤4;
③EC平分∠DCH;④当点H与点A重合时,EF=![]() .
.
以上结论中,你认为正确的有______.(填序号)
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
①ac![]()
②a﹣b+c>0;
③当![]() 时,y随x的增大而增大
时,y随x的增大而增大
若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1
,y2)是抛物线上的两点,则y1![]() y2;
y2;
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
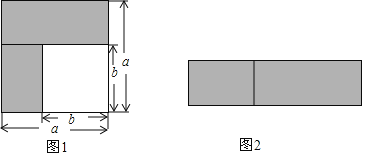
小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作实验;把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,数学来源于生活又服务于生活,利用数学中的知识可以帮助我们解决许多实际问题.如王明想建一个超市,经调查发现他家附近有两个大的居民区![]() ,
,![]() ,同时又有相交的两条公路
,同时又有相交的两条公路![]() ,
,![]() ,为方便进货和居民生活,王明想把超市建在到两居民区的距离相等,同时到两公路距离也相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助王明在图上确定超市的位置!请用尺规作图确定超市点
,为方便进货和居民生活,王明想把超市建在到两居民区的距离相等,同时到两公路距离也相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助王明在图上确定超市的位置!请用尺规作图确定超市点![]() 的位置.(作图不写作法,但要求保留作图痕迹)
的位置.(作图不写作法,但要求保留作图痕迹)
先将实际问题转化为数学问题,把超市看作一个点.
点![]() 到
到![]() ,
,![]() 两点的距离相等,根据性质:__________________, 需用尺规作出_____________;又点
两点的距离相等,根据性质:__________________, 需用尺规作出_____________;又点![]() 到两相交直线
到两相交直线![]() ,
,![]() 的距离相等,根据性质:_________________, 需用尺规作出_______________;而点
的距离相等,根据性质:_________________, 需用尺规作出_______________;而点![]() 同时满足上述两个条件,因此应该是它们的交点.
同时满足上述两个条件,因此应该是它们的交点.
请同学们先完成分析过程(即填空) ,再作图;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ABCD中,AB 6cm ,BC 12cm ,B 30,点P 在 BC 上由点B向点C 出发,速度为每秒2cm;点Q 在边AD上,同时由点 D 向点 A 运动,速度为每秒1cm ,当点 P 运动到点C时,P 、Q 同时停止运动,连接 PQ,设运动时间为t秒.
(1)当t为何值时四边形 ABPQ 为平行四边形?
(2)当t为何值时,四边形 ABPQ 的面积是四边形 ABCD 的面积的四分之三?
(3)连接 AP ,是否存在某一时刻t,使ABP 为等腰三角形?并求出此刻t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C(-1,2)、D(a,1).
(x<0)分别交于点C(-1,2)、D(a,1).
(1)分别求出直线及双曲线的解析式;
(2)利用图象直接写出,当x在什么范围内取值时,y1>y2.
(3)请把直线![]() 上y1<y2时的部分用黑色笔描粗一些.
上y1<y2时的部分用黑色笔描粗一些.
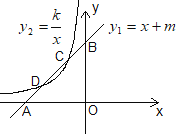
查看答案和解析>>
科目:初中数学 来源: 题型:
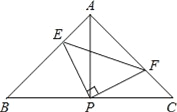
【题目】如图已知在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB和AC于点E、F,给出以下五个结论正确的个数有( )
①AE=CF②∠APE=∠CPF ③△BEP≌△AFP④△EPF是等腰直角三角形⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),S四边形AEPF=![]() S△ABC.
S△ABC.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com