
 如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=$\frac{1}{3}$AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8$\sqrt{3}$,其中正确的结论是①②③(只填序号).
如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=$\frac{1}{3}$AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8$\sqrt{3}$,其中正确的结论是①②③(只填序号). 分析 根据折叠的性质得出BE=PE,∠BEF=∠FPE,EF⊥BP,△EBF的面积=△EPF的面积,再逐个判断即可.
解答 解:∵AE=$\frac{1}{3}$AB=2,
∴AB=3×2=6,BE=6-2=4,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴BE=PE=4,
即AE=$\frac{1}{2}$BE=$\frac{1}{2}$PE,
∵四边形ABCD是矩形,
∴∠ABC=90°,∠A=90°,
∴∠APE=30°,
∴∠AEP=60°,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴∠BEF=∠FPE=$\frac{1}{2}$×(180°-60°)=60°,∠ABC=∠EPF=90°,
∠PFE=∠EFB=180°-90°-60°=30°,
∴EF=2BE,∴①正确;
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴EF⊥BP,
∴∠EQB=90°
在△APE和△QEB中
$\left\{\begin{array}{l}{∠AEP=∠BEQ=60°}\\{∠A=∠EQB=90°}\\{PE=BE}\end{array}\right.$
∴△APE≌△QEB,∴②正确;
∵∠EBF=∠EQB=∠BQF=90°,∠BFE=30°,
∴∠FBQ=90°-30°=60°,∠EBQ=90°-60°=30°,
∴BE=2QE,EF=2BE,
∴EF=4QE,
∴FQ=3EQ,∴③正确;
∵BE=4,∠EBF=90°,∠EFB=30°,
∴BF=$\sqrt{3}$BE=4$\sqrt{3}$,
∴△BEF的面积为$\frac{1}{2}×BE×BF$=$\frac{1}{2}×4×4\sqrt{3}$=8$\sqrt{3}$,
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,
∴△FPE的面积为8$\sqrt{3}$,
∴S四边形BFPE=16$\sqrt{3}$,∴④错误;
故答案为:①②③.
点评 本题考查了矩形的性质,折叠的性质,全等三角形的性质和判定,含30°角的直角三角形的性质等知识点,能综合性运用性质进行推理是解此题的关键,难度偏大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
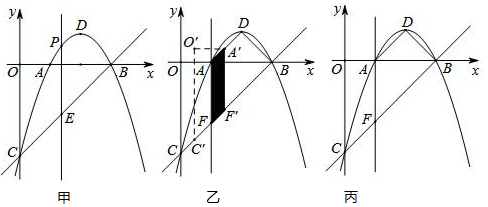
 高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
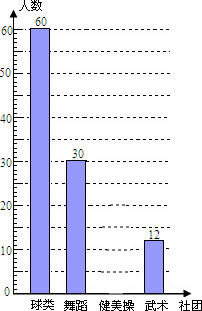 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数比例 |
| 球类 | 60 | m |
| 舞蹈 | 30 | 0.25 |
| 健美操 | n | 0.15 |
| 武术 | 12 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
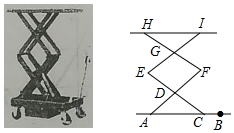 如图是某科技馆展览的一个升降平台模型,在其示意图中,AB=AF=CE=EI=FH=50cm,其中点D是AF和CE的中点,点G是EI和FH的中点.当点C在线段AB上滑动时,∠DAC的大小随之发生变化,平台的高度也随之发生变化,从而控制平台面HI的升降.
如图是某科技馆展览的一个升降平台模型,在其示意图中,AB=AF=CE=EI=FH=50cm,其中点D是AF和CE的中点,点G是EI和FH的中点.当点C在线段AB上滑动时,∠DAC的大小随之发生变化,平台的高度也随之发生变化,从而控制平台面HI的升降.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com