
二次函数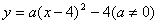 的图象在2<
的图象在2< <3这一段位于
<3这一段位于 轴的下方,在6<
轴的下方,在6< <7这一段位于
<7这一段位于 轴的上方,则
轴的上方,则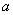 的值为【 】
的值为【 】
A. 1 B. -1 C. 2 D. -2
科目:初中数学 来源: 题型:
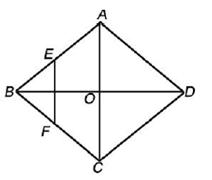
如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF,若
EF=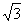 ,BD=4,则菱形ABCD的周长为( ).
,BD=4,则菱形ABCD的周长为( ).
A.4 B. C.
C.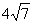 D.28
D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成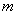 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究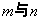 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当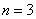 时,
时,
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当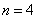 时,
时,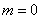
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当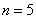 时,
时,
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当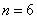 时,
时,
综上所述,可得表①
|
| 3 | 4 | 5 | 6 |
|
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2) 分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
|
| 7 | 8 | 9 | 10 |
|
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用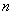 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设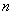 分别等于
分别等于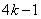 、
、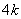 、
、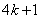 、
、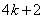 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,若旗杆与教学楼的距离为9m,则旗杆AB的高度是 m(结果保留根号)
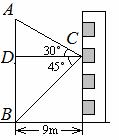
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线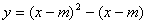 ,其中
,其中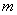 是常数
是常数
(1)求证:不论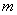 为何值,该抛物线与
为何值,该抛物线与 轴一定有两个公共点;
轴一定有两个公共点;
(2)若该抛物线的对称轴为直线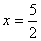 ,
,
①求该抛物线的函数解析式;
②把该抛物线沿 轴向上平移多少个单位长度后,得到的抛物线与
轴向上平移多少个单位长度后,得到的抛物线与 轴只有一个公共点?
轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数
),反比例函数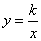 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 利用三角函数求出D点坐标:D(-6,
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 利用三角函数求出D点坐标:D(-6,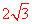 )
)
A.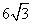 B.
B. C.
C.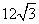 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com