
【题目】如图,△ABC中,∠C=90°,AB=10 cm,BC=6 cm,动点P从点C出发,以每秒2 cm的速度按C→A的路径运动,设运动时间为t秒.
(1)出发2秒时,△ABP的面积为 cm2;
(2)当t为何值时,BP恰好平分∠ABC?

【答案】(1)12;(2) ![]() .
.
【解析】试题分析:(1)利用勾股定理得出AC=8cm,进而表示出AP的长,进而得出答案;
(2)过点P作PD⊥AB于点D,由HL证明Rt△BPD≌Rt△BPC,得出BD=BC=6cm,因此AD=10-6=4cm,设PC=tcm,则PA=(8-t)cm,由勾股定理得出方程,解方程即可.
试题解析:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC=8cm,
根据题意可得:PC=4cm,则AP=4cm,
故△ABP的面积为: ![]() ×AP×BC=
×AP×BC=![]() ×4×6=12(cm2);
×4×6=12(cm2);
(2)解:过点P作PG⊥AB于G,则∠BGP=90°.

∵∠C=90°,
∴∠BGP=∠C.
∵BP平分∠ABC,
∴∠CBP=∠ABP.
又∵BP=BP,
∴△BCP≌△BGP.
∴BG=BC=6,PG=PC=2t.
∴PA=8-2t,AG=10-6=4.
在Rt△APG中, AG2+PG2=AP2.
∴42+(2t)2=(8-2t)2
解得t=![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )
A.(3,5)
B.(-5,3)
C.(3,-5)
D.(-5,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
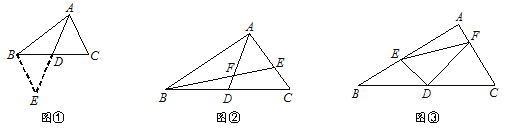
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队计划在10天内修路6km.现计划发生变化,准备8天完成修路任务,那么这8天平均每天至少要修路多少?设这8天平均每天要修路xkm,依题意得一元一次不等式为:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(5,2).
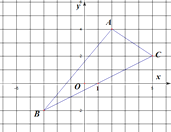
(1)在图中画出△ABC关于y轴对称的△A′B′C′,并写出点A′,B′,C′的坐标;
(2)求△ABC的面积;
(3)在x轴上找点P,使PA+PC的值最小,并观察图形,写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
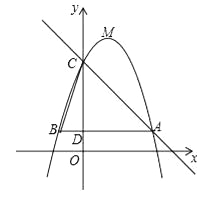
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com