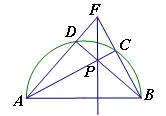
试题分析:(1)连结OC,由PF为切线可得∠OCP=90°,即∠1+∠PCD=90°,由GE⊥AB得∠GEA=90°,则∠2+∠ADE=90°,利用∠1=∠2得到∠PCD=∠ADE,根据对顶角相等得∠ADE=∠PDC,所以∠PCD=∠PDC,于是根据等腰三角形的判定定理得到△PCD是等腰三角形;
(2)连结OD,BG,在Rt△COF中根据含30度的直角三角形三边的关系可计算出OC=2,由于∠FOC=90°,∠F=30°,所以∠FOC=60°,由三角形外角性质可知∠1=∠2=30°,则∠PCD=90°﹣∠1=60°,从而△PCD为等边三角形;再由D为AC的中点,由垂径定理得到OD⊥AC,AD=CD,在Rt△OCD中,可得OD=
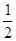
OC=1,CD=
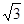
OD=
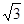
,所以△PCD的周长为3
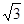
;然后在Rt△ADE中,可得DE=
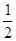
AD=
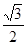
,AE=
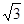
DE=
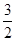
,由AB为直径得到∠AGB=90°,再证明Rt△AGE∽Rt△ABG,利用相似比可计算出AG.
试题解析:(1)连结OC,如图,
∵PC为⊙O的切线,
∴OC⊥PC,
∴∠OCP=90°,即∠1+∠PCD=90°,
∵GE⊥AB,
∴∠GEA=90°,
∴∠2+∠ADE=90°,
∵OA=OC,
∴∠1=∠2,
∴∠PCD=∠ADE,
而∠ADE=∠PDC,
∴∠PCD=∠PDC,
∴△PCD是等腰三角形;
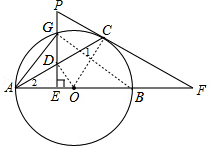
(2)连结OD,BG,如图,
在Rt△COF中,∠F=30°,BF=2,
∴OF=2OC,即OB+2=2OC,
而OB=OC,
∴OC=2,
∵∠FOC=90°﹣∠F=60°,
∴∠1=∠2=30°,
∴∠PCD=90°﹣∠1=60°,
∴△PCD为等边三角形,
∵D为AC的中点,
∴OD⊥AC,
∴AD=CD,
在Rt△OCD中,OD=
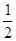
OC=1,
CD=
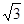
OD=
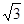
,
∴△PCD的周长为3
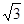
;
在Rt△ADE中,AD=CD=
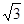
,
∴DE=
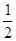
AD=
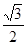
,
AE=
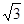
DE=
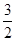
,
∵AB为直径,
∴∠AGB=90°,
而∠GAE=∠BAG,
∴Rt△AGE∽Rt△ABG,
∴AG:AB=AE:AG,
∴AG
2=AE•AB=
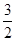
×4=6,
∴AG=6.

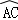 上一点,GE⊥AB,垂足为点E,交AC于点D,过点C的切线与AB的延长线交于点F,与EG的延长线交于点P,连接AG.
上一点,GE⊥AB,垂足为点E,交AC于点D,过点C的切线与AB的延长线交于点F,与EG的延长线交于点P,连接AG.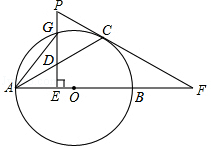
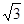 ;AG=6
;AG=6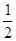 OC=1,CD=
OC=1,CD=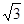 OD=
OD=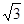 ,所以△PCD的周长为3
,所以△PCD的周长为3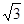 ;然后在Rt△ADE中,可得DE=
;然后在Rt△ADE中,可得DE=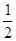 AD=
AD=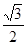 ,AE=
,AE=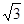 DE=
DE=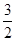 ,由AB为直径得到∠AGB=90°,再证明Rt△AGE∽Rt△ABG,利用相似比可计算出AG.
,由AB为直径得到∠AGB=90°,再证明Rt△AGE∽Rt△ABG,利用相似比可计算出AG.
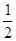 OC=1,
OC=1,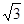 OD=
OD=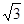 ,
,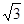 ;
;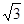 ,
,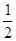 AD=
AD=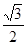 ,
,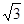 DE=
DE=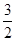 ,
,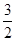 ×4=6,
×4=6,

 名校课堂系列答案
名校课堂系列答案 的长.
的长.