
【题目】如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,
①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.
【答案】
(1)
【解答】解:猜想:筝形对角线之间的位置关系:垂直.即OT⊥MN.
证明:连接OT,MN,
在△OMT和△ONT中,
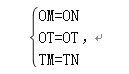 ,
,
∴△OMT≌△ONT(SSS),
∴∠MOT=∠NOT,
∵OM=ON,
∴OT⊥MN(等腰三角形三线合一).
(2)
【解答】
①存在.
由(1)得AC⊥BD,设AC与BD交于点M,
在Rt△AMB中,AB=5,BM=![]() BD=4,
BD=4,
∴AM=![]() =3,
=3,
∵A、B、C、D四点共圆,
∴∠ABC+∠ADC=180°,
又∵△ABC≌△ADC,
∴∠ABC=∠ADC=90°,
∴AC即为所求圆的直径
∵∠BAM=∠BAC,∠ABC=∠AMB=90°,
∴△ABM∽△ACB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AC=![]()
∴圆的半径为:![]() AC=
AC=![]() .
.
②作FM⊥AB,作EG⊥AB于G.
∵四边形ABED是菱形,
∴AE⊥BD,且BN=![]() BD=4,
BD=4,
∴AN=NE=![]() =
=![]() =3,AE=6.
=3,AE=6.
∴S菱形ABED=![]() AEBD=
AEBD=![]() ×6×8=24,
×6×8=24,
又∵S菱形ABED=ABEG,
∴EG=![]() .
.
∵∠DBF=∠DBF,∠BNE=∠BFD,
∴△BNE∽△BFD,
∴![]() ,即
,即![]() ,
,
∴BF=![]() .
.
∵GE⊥AB,FM⊥AB,
∴GE∥FM,
∴△BEG∽△BFM,
∴![]() ,即
,即![]() ,
,
解得:FM=![]() .
.
【解析】(1)证明△OMP≌△ONP,即可证得MN⊥OT,且OT平分MN;
(2)①若经过A,B,C,D四个点的圆存在,则对角互补,据此即可判断;
②已知FM⊥AB,作EG⊥AB于G,根据菱形的面积公式求得GE的长,然后根据△BNE∽△BFD求得BF的长,再根据△BEG∽△BFM求得FM的长.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在甲口袋中有三张完全相同的卡片,分别标有﹣1,1,2,乙口袋中有完全相同的卡片,分别标有﹣2,3,4,从这两个口袋中各随机取出一张卡片.
(1)用树状图或列表表示所有可能出现的结果;
(2)求两次取出卡片的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | a |
200<x≤400 | b |
x>400 | 0.92 |
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=![]() 的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
(1)求k的值.
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11月读书节,深圳市为统计某学校初三学生读书状况,如下图:
(1)求三本以上的x值、参加调查的总人数,并补全统计图;
(2)三本以上的圆心角为 ° .
(3)全市有6.7万学生,三本以上有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n﹣1,![]() )
)
B.(2n﹣1,![]() )
)
C.(4n+1,![]() )
)
D.(2n+1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com