
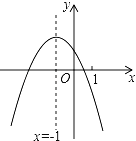
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②2a﹣b=0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中说法正确的有_____.
【答案】①②④
【解析】
根据二次函数的图象可知抛物线与x轴有两个交点,对称轴为x=﹣1,二次函数图象具有对称性,从而可以判断题目中的结论是否正确.
解:∵由图象可知,当y=0时,图象与x轴有两个交点,
∴ax2+bx+c=0时,b2﹣4ac>0.
∴4ac﹣b2<0.(故①正确);
∵二次函数的对称轴:![]()
∴b=2a.
∴2a﹣b=0.(故②正确);
∵由图象可知,x=0时和x=﹣2时函数值相等,都大于零,
∴x=﹣2时,y=4a﹣2b+c>0.
∴4a+c>2b.(故③错误);
∵由图象可知x=﹣1时该二次函数取得最大值,
∴a﹣b+c>am2+bm+c(m≠﹣1).
∴m(am+b)<a﹣b.(故④正确)
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】某校图书馆为了满足同学们阅读课外书的需求,计划购进甲、乙两种图书共100套,其中甲种图书每套120元,乙种图书每套80元.设购买甲种图书的数量![]() 套.
套.
(1)按计划用11000元购进甲、乙两种图书时,问购进这甲、乙两种图书各多少套?
(2)若购买甲种图书的数量要不少于乙种图书的数量的![]() ,购买两种图书的总费用为
,购买两种图书的总费用为![]() 元,求出最少总费用.
元,求出最少总费用.
(3)图书馆在不增加购买数量的情况下,增加购买丙种图书,要求甲种图书与丙种图书的购买费用相同.丙种图书每套100元,总费用比(2)中最少总费用多出1240元,请直接写出购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
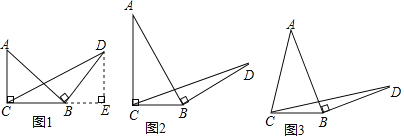
![]() 探究1:如图1,在等腰直角三角形ABC中,
探究1:如图1,在等腰直角三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 求证:
求证:![]() 的面积为
的面积为![]() 提示:过点D作BC边上的高DE,可证
提示:过点D作BC边上的高DE,可证![]() ≌
≌![]()
![]() 探究2:如图2,在一般的
探究2:如图2,在一般的![]() 中,
中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 请用含a的式子表示
请用含a的式子表示![]() 的面积,并说明理由.
的面积,并说明理由.
![]() 探究3:如图3,在等腰三角形ABC中,
探究3:如图3,在等腰三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 试探究用含a的式子表示
试探究用含a的式子表示![]() 的面积,要有探究过程.
的面积,要有探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线C1:y=﹣(x+m)2+m2(m>0),抛物线C2:y=(x﹣n)2+n2(n>0),称抛物线C1,C2互为派对抛物线,例如抛物线C1:y=﹣(x+1)2+1与抛物线C2:y=(x﹣![]() )2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
)2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
(1)已知抛物线①y=﹣x2﹣2x,②y=(x﹣3)2+3,③y=(x﹣![]() )2+2,④y=x2﹣x+
)2+2,④y=x2﹣x+![]() ,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
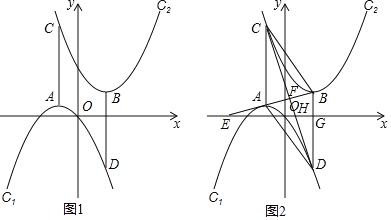
(2)如图1,当m=1,n=2时,证明AC=BD;
(3)如图2,连接AB,CD交于点F,延长BA交x轴的负半轴于点E,记BD交x轴于G,CD交x轴于点H,∠BEO=∠BDC.
①求证:四边形ACBD是菱形;
②若已知抛物线C2:y=(x﹣2)2+4,请求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
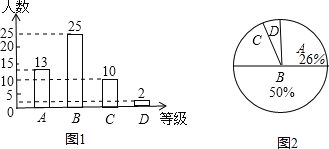
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com