
【题目】已知在正方形ABCD中,点E、F分别为边BC与CD上的点,且∠EAF=45°,AE与AF分别交对角线BD于点M、N,则下列结论正确的是_____.
①∠BAE+∠DAF=45°;②∠AEB=∠AEF=∠ANM;③BM+DN=MN;④BE+DF=EF
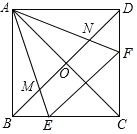
【答案】①②④
【解析】
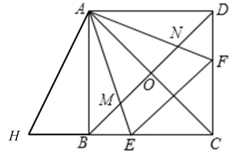
由∠EAF=45°,可得∠BAE+∠DAF=45°,故①正确;如图,把△ADF绕点A顺时针旋转90°得到△ABH,根据三角形的外角的性质得到∠ANM=∠AEB,于是得到∠AEB=∠AEF=∠ANM;故②正确;由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,由已知条件得到∠EAH=∠EAF=45°,根据全等三角形的性质得到EH=EF,∴∠AEB=∠AEF,求得BE+BH=BE+DF=EF,故④正确;BM、DN、MN存在BM2+DN2=MN2的关系,故③错误.
解:∵∠EAF=45°,∴∠BAE+∠DAF=45°,故①正确;
如图,把△ADF绕点A顺时针旋转90°得到△ABH,
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°-∠EAF=45°,
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
 ,
,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,
∴BE+BH=BE+DF=EF,故④正确;
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°-∠BAE=90°-(∠HAE-∠BAH)=90°-(45°-∠BAH)=45°+∠BAH,
∴∠ANM=∠AEB,
∴∠AEB=∠AEF=∠ANM;故②正确;
BM、DN、MN满足等式BM2+DN2=MN2,而非BM+DN=MN,故③错误.
故答案为①②④.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车已知该型号汽车的进价为10万元/辆,经销一段时间后发现:当该型号汽车售价定为20万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆
(1)若每辆汽车的售价降低x万元,则每周的销售量是 辆(用含x的代数式表示)
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,需将每辆汽车的售价降低多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月份,我市迎来国家级文明城市复查,为了了解学生对文明城市的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解![]() 了解
了解![]() 了解较少
了解较少![]() 不了解”四类分别统计,并绘制了下列两幅统计图(不完整
不了解”四类分别统计,并绘制了下列两幅统计图(不完整![]() 请根据图中信息,解答下列问题:
请根据图中信息,解答下列问题:
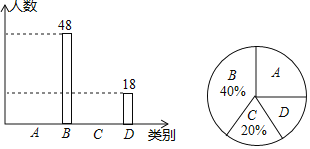
![]() 此次共调查了______名学生;
此次共调查了______名学生;
![]() 扇形统计图中D所在的扇形的圆心角为______;
扇形统计图中D所在的扇形的圆心角为______;
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 若该校共有800名学生,请你估计对文明城市的了解情况为“非常了解”的学生的人数.
若该校共有800名学生,请你估计对文明城市的了解情况为“非常了解”的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2﹣2ax+4a+2(a是常数),
(Ⅰ)若该抛物线与x轴的一个交点为(﹣1,0),求a的值及该抛物线与x轴另一交点坐标;
(Ⅱ)不论a取何实数,该抛物线都经过定点H.
①求点H的坐标;
②证明点H是所有抛物线顶点中纵坐标最大的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
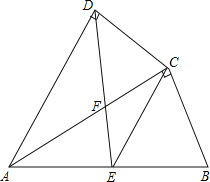
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
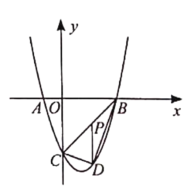
【题目】在平面直角坐标系中,抛物线![]() 经过点A、B、C,已知A(-1,0),B(3,0),C(0,-3).
经过点A、B、C,已知A(-1,0),B(3,0),C(0,-3).
(1)求此抛物线的函数表达式;
(2)若P为线段BC上一点,过点P作![]() 轴的平行线,交抛物线于点D,当△BCD面积最大时,求点P的坐标;
轴的平行线,交抛物线于点D,当△BCD面积最大时,求点P的坐标;
(3)若M(m,0)是![]() 轴上一个动点,请求出CM+
轴上一个动点,请求出CM+![]() MB的最小值以及此时点M的坐标.
MB的最小值以及此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
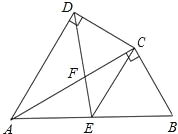
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
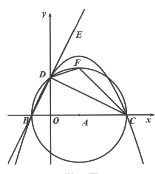
【题目】如图,已知点B的坐标是(-2,0),点C的坐标是(8,0),以线段BC为直径作⊙A,交y轴的正半轴于点D,过B、C、D三点作抛物线.
(1)求抛物线的解析式;
(2)连结BD,CD,点E是BD延长线上一点,∠CDE的角平分线DF交⊙A于点F,连结CF,在直线BE上找一点P,使得△PFC的周长最小,并求出此时点P的坐标;
(3)在(2)的条件下,抛物线上是否存在点G,使得∠GFC=∠DCF,若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中国数学名著《九章算术》中,有这样一个问题:“今有共买牛,七家共出一百九十,不足三百三十;九家共出二百七十,盈三十. 问家数、牛价各几何?”大意是:几家人凑钱合伙买牛,如果每7家共出190元,那么还缺少330元钱;如果每9家共出270元,又多了30元钱. 问共有多少人家,每头牛的价钱是多少元?若设有x户人家,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com