
【题目】在平面直角坐标系中,已知抛物线y=x2﹣2ax+4a+2(a是常数),
(Ⅰ)若该抛物线与x轴的一个交点为(﹣1,0),求a的值及该抛物线与x轴另一交点坐标;
(Ⅱ)不论a取何实数,该抛物线都经过定点H.
①求点H的坐标;
②证明点H是所有抛物线顶点中纵坐标最大的点.
【答案】(Ⅰ)a=﹣![]() ,抛物线与x轴另一交点坐标是(0,0);(Ⅱ)①点H的坐标为(2,6);②证明见解析.
,抛物线与x轴另一交点坐标是(0,0);(Ⅱ)①点H的坐标为(2,6);②证明见解析.
【解析】
(I)根据该抛物线与x轴的一个交点为(-1,0),可以求得的值及该抛物线与x轴另一交点坐标;
(II)①根据题目中的函数解析式可以求得点H的坐标;
②将题目中的函数解析式化为顶点式,然后根据二次函数的性质即可证明点H是所有抛物线顶点中纵坐标最大的点.
(Ⅰ)∵抛物线y=x2﹣2ax+4a+2与x轴的一个交点为(﹣1,0),
∴0=(﹣1)2﹣2a×(﹣1)+4a+2,
解得,a=﹣![]() ,
,
∴y=x2+x=x(x+1),
当y=0时,得x1=0,x2=﹣1,
即抛物线与x轴另一交点坐标是(0,0);
(Ⅱ)①∵抛物线y=x2﹣2ax+4a+2=x2+2﹣2a(x﹣2),
∴不论a取何实数,该抛物线都经过定点(2,6),
即点H的坐标为(2,6);
②证明:∵抛物线y=x2﹣2ax+4a+2=(x﹣a)2﹣(a﹣2)2+6,
∴该抛物线的顶点坐标为(a,﹣(a﹣2)2+6),
则当a=2时,﹣(a﹣2)2+6取得最大值6,
即点H是所有抛物线顶点中纵坐标最大的点.


科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求8名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径AB的延长线上,且∠CDB=∠CAD,过点A作⊙O的切线,交CD的延长线于点E.

(1)判定直线CD与⊙O的位置关系,并说明你的理由;
(2)若CB=4,CD=8,①求圆的半径.②求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
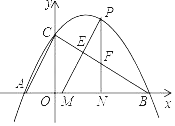
【题目】如图,二次函数y=ax2+bx+![]() 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)求这个二次函数的解析式;
(2)求线段PE最大值,并求出线段PE最大时点P的坐标;
(3)若S△PMN=3S△PEF时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(2,5),C(4,2)(每个方格的边长均为1个单位长度)
(1)将△ABC平移,使点A移动到点A1,请画出△A1B1C1;
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标;
(3)△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
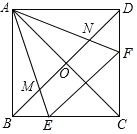
【题目】已知在正方形ABCD中,点E、F分别为边BC与CD上的点,且∠EAF=45°,AE与AF分别交对角线BD于点M、N,则下列结论正确的是_____.
①∠BAE+∠DAF=45°;②∠AEB=∠AEF=∠ANM;③BM+DN=MN;④BE+DF=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为( )
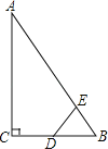
A.4或5B.4或7C.4或5或7D.4或7或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1 cm.参考数据: sin75°="0.966," cos75°=0.259,tan75°=3.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com