
【题目】如图1,抛物线![]() 与两条坐标轴分别交于
与两条坐标轴分别交于![]() ,
,![]() ,
,![]() 三点.其中
三点.其中![]() ,且
,且![]() .
.
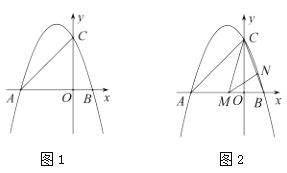
(1)求该抛物线的解析式;
(2)点![]() 是
是![]() 轴上一点,抛物线上是否存在点
轴上一点,抛物线上是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为边的四边形是平行四边形?若存在,求出点
为边的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点,连接
上的动点,连接![]() ,
,![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ,
,![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)根据![]() ,且
,且![]() ,得到点A的坐标,代入A和C的坐标即可求解;
,得到点A的坐标,代入A和C的坐标即可求解;
(2)该平行四边形以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为边,且Q在x轴上,设点
为边,且Q在x轴上,设点![]() 的坐标为
的坐标为![]() ,根据平行四边形的性质可得
,根据平行四边形的性质可得![]() ,求解即可;
,求解即可;
(3)由![]() 得到
得到![]() 平分
平分![]() ,故过点
,故过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,可得
,可得![]() ,并可用含m的代数式表示线段长度,通过证明得到
,并可用含m的代数式表示线段长度,通过证明得到![]() ,对应线段成比例可求得m的值,再证明
,对应线段成比例可求得m的值,再证明![]() ,并表示各自的正切值,即可求解.
,并表示各自的正切值,即可求解.
(1)∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]()
代入可得:![]() ,
,
解得:![]() ,∴
,∴![]() .
.
(2)存在,设点![]() 的坐标为
的坐标为![]() ,依题意有
,依题意有
![]()
当![]() 时,解得
时,解得![]() ,
,![]() (舍去),
(舍去),
∴![]()
当![]() 时,解得
时,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
(3)抛物线![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() 平分
平分![]() ,
,
过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即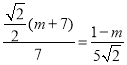 ,
,
解得:![]() ,∴
,∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,易得
,易得![]() ,
,
![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() .
.
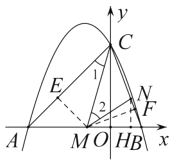
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵ ,
,
∴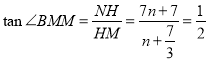 ,
,
解得:![]() ,
,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】我市某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、五个组,
、五个组,![]() 表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
![]() 组:
组:![]()
![]() 组:
组:![]()
![]() 组:
组:![]()
![]() 组:
组:![]()
![]() 组:
组:![]()
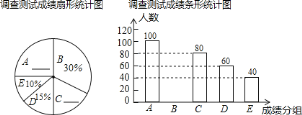
![]() 参加调查测试的学生共有________人;请将两幅统计图补充完整.
参加调查测试的学生共有________人;请将两幅统计图补充完整.
![]() 本次调查测试成绩的中位数落在________组内.
本次调查测试成绩的中位数落在________组内.
![]() 本次调查测试成绩在
本次调查测试成绩在![]() 分以上(含
分以上(含![]() 分)为优秀,该中学共有
分)为优秀,该中学共有![]() 人,请估计全校测试成绩为优秀的学生有多少人?
人,请估计全校测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交x轴、y轴于A,B两点,经过A,B两点的抛物线
分别交x轴、y轴于A,B两点,经过A,B两点的抛物线![]() 与x轴的正半轴相交于点
与x轴的正半轴相交于点![]() .
.

(1)求抛物线的解析式;
(2)若P为线段AB上一点,![]() ,求AP的长;
,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)若![]() 的面积为
的面积为![]() 的面积的2倍,求此直线的函数表达式.
的面积的2倍,求此直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积![]() 来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积
来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积![]() 来近似估计半径为1的⊙O的面积,则
来近似估计半径为1的⊙O的面积,则![]() ____.(结果保留根号)
____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):

(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,校文学社为了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
收集数据:从学校随机抽取20名,进行了每周用于课外阅读时间的调查,数据如下(单位:![]() ):
):
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分数段整理样本数据并补全表格:
|
|
|
| |
等级 |
|
|
|
|
人数 | 3 |
| 8 | 4 |
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论:
(1)请写出表中![]() _________;
_________;![]() _________
_________![]() ;
;![]() __________
__________![]() ;
;
(2)如果该校现有学生7500人,估计等级为“![]() ”的学生有_________名;
”的学生有_________名;
(3)假设平均阅读一本课外书的时间为![]() ,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)试证明DE是⊙O的切线;
(2)若⊙O的半径为5,AC=6![]() ,求此时DE的长.
,求此时DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店经销A、B两种水果,A种水果进货单价比B种水果进货单价多2元,花50元购进A种水果的数量与花40元购进B种水果的数量相同.在销售过程中发现,A种水果每天销售量是![]() 与销售价x(元)满足关系式
与销售价x(元)满足关系式![]() ,B种水果,每天销售量
,B种水果,每天销售量![]() 与销售价x(元)满足
与销售价x(元)满足![]() = -x+14
= -x+14
(1)求A、B两种水果的单价.
(2)已知A种水果比B种水果的销售价高2元/千克,且每天A、B水果均有a千克坏掉.设B水果售价为t元/千克,每天两种水果的总利润为W元,求W与t的函数解析式,并求出当a的取值在什么范围内,水果店有可能不赔钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com