
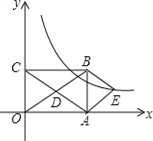
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,即可证出四边形AEBD是菱形;
(2)连接DE,交AB于F,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;设经过点E的反比例函数解析式为:y=![]() ,把点E坐标代入求出k的值即可.
,把点E坐标代入求出k的值即可.
(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=![]() AC,DB=
AC,DB=![]() OB,AC=OB,AB=OC=2,
OB,AC=OB,AB=OC=2,
∴DA=DB,
∴四边形AEBD是菱形;
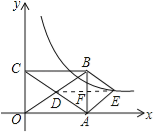
(2)解:连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=![]() OA=
OA=![]() ,AF=
,AF=![]() AB=1,3+
AB=1,3+![]() =
=![]() ,
,
∴点E坐标为:(![]() ,1),
,1),
设经过点E的反比例函数解析式为:y=![]() ,
,
把点E(![]() ,1)代入得:k=
,1)代入得:k=![]() ,
,
∴经过点E的反比例函数解析式为:y=![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】某种商品原价是100元,经两次降价后的价格是90元.设平均每次降价的百分率为x,可列方程为( )
A.100x(1﹣2x)=90
B.100(1+2x)=90
C.100(1﹣x)2=90
D.100(1+x)2=90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.﹣a+b+c+d=﹣(a﹣b)﹣(﹣c﹣d)
B.x﹣(y﹣z)=x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣(x﹣y+z)=﹣x﹣y﹣z
查看答案和解析>>
科目:初中数学 来源: 题型:
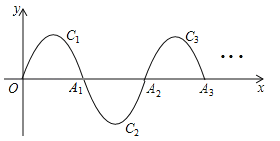
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
查看答案和解析>>
科目:初中数学 来源: 题型:
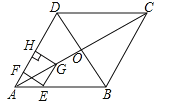
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为 ;当OO′⊥AD时,t的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com