
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ���һö���ؼ��Σ�������˼�ǣ����м��ִ�����װ�лƽ�9ö��ÿö�ƽ�������ͬ�������ִ�����װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö���ִ��ӱ����ִ�������13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض���������ÿö�ƽ���x����ÿö������y������ɽ�������Ϊ��������
A.![]() B.
B.![]()
C.![]() D.
D.![]()

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
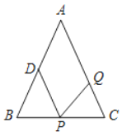
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е㣮��
���е㣮��![]() ���߶�
���߶�![]() ����
����![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ���
���![]() �˶���ͬʱ����
�˶���ͬʱ����![]() ���߶�
���߶�![]() ���ɵ�
���ɵ�![]() ���
���![]() �˶��������˶���ʱ��Ϊ
�˶��������˶���ʱ��Ϊ![]() �����
�����![]() ���˶��ٶ�Ϊ
���˶��ٶ�Ϊ![]() ����ʹ��
����ʹ��![]() ����
����![]() ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ӣ����![]() ������־�����30���ֻ������˼�⣬��������н��ķ�֮һ���ֻ�Я����ϸ�������ﵽ�ɽ���������10��������һ��������ֻ�һ�����������˳��������������������ֻ��Ϸ��ֵ��к�ϸ���У���Ϊ�������к�ϸ���������ɫ�������������ϸ���ɵ���һϵ�и�Ⱦ�����ɫ�������Ϊ���Σ�ֱ��
������־�����30���ֻ������˼�⣬��������н��ķ�֮һ���ֻ�Я����ϸ�������ﵽ�ɽ���������10��������һ��������ֻ�һ�����������˳��������������������ֻ��Ϸ��ֵ��к�ϸ���У���Ϊ�������к�ϸ���������ɫ�������������ϸ���ɵ���һϵ�и�Ⱦ�����ɫ�������Ϊ���Σ�ֱ��![]() ���ң�0��0000008��������ÿ�ѧ��������ʾΪ�� ��
���ң�0��0000008��������ÿ�ѧ��������ʾΪ�� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ķ��������ѧС̽��ϵ�У��������������⣺
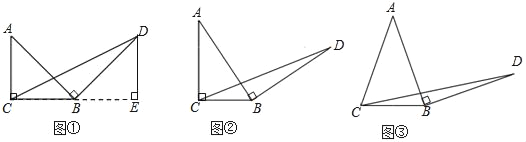
��1��̽��1����ͼ�٣��ڵ���ֱ��������ABC�У���ACB��90�㣬BC��3������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD������D��BC���ϵĸ�DE����DE��BC��������ϵ���� ������BCD�����Ϊ�� ����
��2��̽��2����ͼ�ڣ���һ���Rt��ABC�У���ACB��90�㣬BC��a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD�����ú�a��ʽ�ӱ�ʾ��BCD���������˵�����ɣ�
��3��̽��3����ͼ�ۣ��ڵ���������ABC�У�AB��AC��BC��a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD����̽���ú�a��ʽ�ӱ�ʾ��BCD�������Ҫ��̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
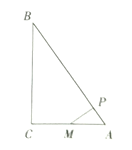
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AM=CM��MP��AB�ڵ�P.��֤��BP2=AP2+BC2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y1=ax2+bx��4��a��0����x�ύ�ڵ�A����1��0���͵�B��4��0����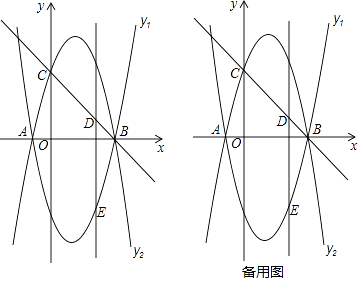
��1����������y1�ĺ�������ʽ��
��2����ͼ�٣���������y1��x�ᷭ�۵õ�������y2 �� ������y2��y�ύ�ڵ�C����D���߶�BC�ϵ�һ�����㣬����D��DE��y�ύ������y1�ڵ�E�����߶�DE�ij��ȵ����ֵ��
��3���ڣ�2���������£����߶�DE���ڳ������ֵλ��ʱ�����߶�BC�Ĵ�ֱƽ���߽�DE�ڵ�F������ΪH����P��������y2��һ���㣬��P��ֱ��BC���У���S��P��S��DFH=2�У����������������е�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
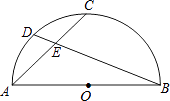
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������C�� ![]() ���е㣬��D��
���е㣬��D�� ![]() ���е㣬����AC��BD���ڵ�E����
���е㣬����AC��BD���ڵ�E���� ![]() =�� ��
=�� ��
A.![]()
B.![]()
C.1�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���п���������ǰ��ij��������Ϊ���˽�ѡ���������ϵij��������ijɼ�������������˱�������ѡ������������Ŀ�ij��������ijɼ����������Եõ��ijɼ����������������������ͳ��ͼ��
�������ͼ�е���Ϣ������������⣺
��![]() ��д������ͼ��
��д������ͼ��![]() __________
__________![]() ������ȫ����ͼ��
������ȫ����ͼ��
��![]() ������γ���У����Գɼ�����������λ���ֱ���__________����__________����
������γ���У����Գɼ�����������λ���ֱ���__________����__________����
��![]() �����������п�ѡ���������ϵ���������
�����������п�ѡ���������ϵ���������![]() �ˣ���������п��������ϴ�
�ˣ���������п��������ϴ�![]() �����ϣ���
�����ϣ���![]() ���������֣�������Ƹ��������п���ѡ���������ϵ������ܻ�����ֵ��ж�������
���������֣�������Ƹ��������п���ѡ���������ϵ������ܻ�����ֵ��ж�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
��1������ͼ�ٵ�������ABCD�ĶԽ���BD����һ��P��ʹPA+PC��С��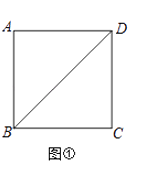
��2����ͼ�ڣ���PΪ����ABCD�ĶԽ���BD��һ���㣬AB=2��BC=2 ![]() ����EΪBC�ߵ��е㣬����һ��P��ʹPE+PC��С�����������Сֵ��
����EΪBC�ߵ��е㣬����һ��P��ʹPE+PC��С�����������Сֵ��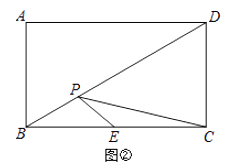
��3����ͼ�ۣ���ʦ����һ��߳�Ϊ1000������ABCD��ժ��AC=1200�ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ��������ĵ�Pλ�ã�����������̾��룻�������ڣ���˵�����ɣ�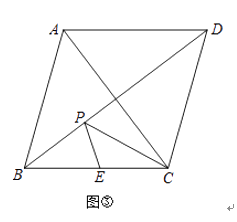
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com