
【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
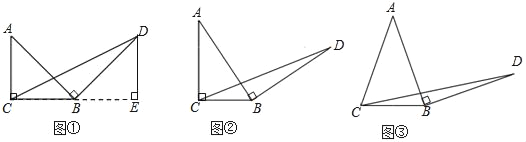
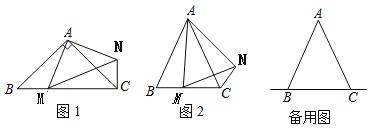
(1)探究1,如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D做BC边上的高DE,则DE与BC的数量关系是 ,△BCD的面积为 ;
(2)探究2,如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由;
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
【答案】(1)DE=BC,△BCD的面积为![]() ;(2)△BCD的面积为
;(2)△BCD的面积为![]() ,理由详见解析;(3)△BCD的面积为
,理由详见解析;(3)△BCD的面积为![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)如图1,过点D作BC的垂线,与BC的延长线交于点E,由垂直的性质就可以得出△ABC≌△BDE,就有DE=BC=3.进而由三角形的面积公式得出结论;
(2)如图2,过点D作BC的垂线,与BC的延长线交于点E,由垂直的性质就可以得出△ABC≌△BDE,就有DE=BC=a.进而由三角形的面积公式得出结论;
(3)如图3,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,由等腰三角形的性质可以得出BF![]() BC,由条件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面积公式就可以得出结论.
BC,由条件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面积公式就可以得出结论.
(1)如图1,过点D作DE⊥CB交CB的延长线于E,∴∠BED=∠ACB=90°,由旋转知:AB=BD,∠ABD=90°,∴∠ABC+∠DBE=90°.
∵∠A+∠ABC=90°,∴∠A=∠DBE.
在△ABC和△BDE中,∵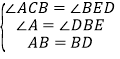 ,∴△ABC≌△BDE(AAS),∴BC=DE=3.
,∴△ABC≌△BDE(AAS),∴BC=DE=3.
∵S△BCD![]() BCDE,∴S△BCD
BCDE,∴S△BCD![]() ×32=
×32=![]() ;
;
(2)△BCD的面积为![]() .理由如下:
.理由如下:
如图2,过点D作BC的垂线,与BC的延长线交于点E,∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BE,∴AB=BD,∠ABD=90°,∴∠ABC+∠DBE=90°.
∵∠A+∠ABC=90°,∴∠A=∠DBE.
在△ABC和△BDE中,∵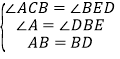 ,∴△ABC≌△BDE(AAS),∴BC=DE=a.
,∴△ABC≌△BDE(AAS),∴BC=DE=a.
∵S△BCD![]() BCDE,∴S△BCD
BCDE,∴S△BCD![]() ;
;
(3)如图3,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,∴∠AFB=∠E=90°,BF![]() BC
BC![]() a,∴∠FAB+∠ABF=90°.
a,∴∠FAB+∠ABF=90°.
∵∠ABD=90°,∴∠ABF+∠DBE=90°,∴∠FAB=∠EBD.
∵线段BD是由线段AB旋转得到的,∴AB=BD.
在△AFB和△BED中,∵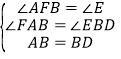 ,∴△AFB≌△BED(AAS),∴BF=DE
,∴△AFB≌△BED(AAS),∴BF=DE![]() a.
a.
∵S△BCD![]() BCDE
BCDE![]()
![]() aa
aa![]() a2,∴△BCD的面积为
a2,∴△BCD的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】在等腰![]() 中,
中,![]() ,点
,点![]() 是直线
是直线![]() 上一点(不与
上一点(不与![]() 重合),以
重合),以![]() 为一边在
为一边在![]() 的右侧作等腰
的右侧作等腰![]() ,使
,使![]() ,
,![]() ,连结
,连结![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上时,如果
上时,如果![]() ,则
,则![]() _______°.
_______°.
(2)设![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上移动时,
上移动时,![]() 之间有怎样的数量关系?请说明理由.
之间有怎样的数量关系?请说明理由.
②当点![]() 在直线
在直线![]() 上移动时,
上移动时,![]() 之间有怎样的数量关系?请你直接写出你的结论.
之间有怎样的数量关系?请你直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“两果问价”问题出自我国古代算书《四元玉鉴》,原题如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个?又问各该几个钱?将题目译成白话文,内容如下:九百九十九文钱买了甜果和苦果共一千个,已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=_____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=﹣x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.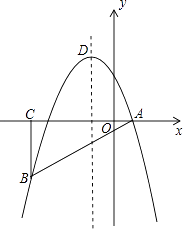
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
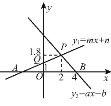
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:今有甲种袋子中装有黄金9枚(每枚黄金重量相同),乙种袋子中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲种袋子比乙种袋子轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,则可建立方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com