
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABCΪ����ֱ�������Σ���ACB=90�㣬������y=��x2+bx+c����A��B���㣬���е�A��C������ֱ�Ϊ��1��0��������4��0���������ߵĶ���Ϊ��D��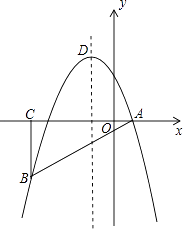
��1���������ߵĽ���ʽ��
��2����E��ֱ��������ABCб��AB�ϵ�һ�����㣨����A��B�غϣ�������E��x��Ĵ��ߣ����������ڵ�F�����߶�FE�ij������ʱ�����E�����ꣻ
��3���ڣ�2���������£����������Ƿ����һ��P��ʹ��PEF����EFΪֱ�DZߵ�ֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��A��C������ֱ�Ϊ��1��0��������4��0����
��AC=5��
�ߡ�ABCΪ����ֱ�������Σ���C=90�㣬
��BC=AC=5��
��B����4����5����
����A�͵�B���������ã� ![]() ����ã�
����ã� ![]() ��
��
�������ߵĽ���ʽΪy=��x2��2x+3��
��2���⣺��ͼ1��ʾ��
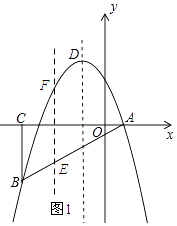
��ֱ��AB�Ľ���ʽΪy=kx+b������A�͵�B���������ã� ![]() ����ã�k=1��b=��1��
����ã�k=1��b=��1��
����ֱ��AB�Ľ���ʽΪy=x��1��
���E��������t��t��1�������F��������t����t2��2t+3����
��EF=��t2��2t+3����t��1��=��t2��3t+4=��t+ ![]() ��2+
��2+ ![]() ��
��
�൱t=�� ![]() ʱ��FEȡ���ֵ
ʱ��FEȡ���ֵ ![]() ����ʱ����E������Ϊ����
����ʱ����E������Ϊ���� ![]() ����
���� ![]() ����
����
��3���⣺���ڵ�P����ʹ��PEF����EFΪֱ�DZߵ�ֱ�������Σ�
���ɣ���ͼ��ʾ������F��ֱ��a��EF�����������ڵ�P������E��ֱ��b��EF����������P�䡢P�壮
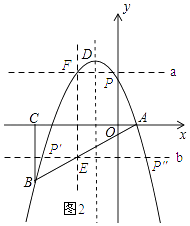
�ɣ�2����֪��E������Ϊ��t��t��1�������F������Ϊ��t����t2��2t+3����t=�� ![]() ��
��
���E���� ![]() ����
���� ![]() ����F����
����F���� ![]() ��
�� ![]() ����
����
�ٵ���t2��2t+3= ![]() ʱ����ã�x=��
ʱ����ã�x=�� ![]() ��x=��
��x=�� ![]() ����ȥ����
����ȥ����
���P���������� ![]() ��
�� ![]() ����
����
�ڵ���t2��2t+3=�� ![]() ʱ����ã�x=��1+
ʱ����ã�x=��1+ ![]() ��x=��1��
��x=��1�� ![]() ��
��
���P�䣨��1�� ![]() ����
���� ![]() ����P�壨��1+
����P�壨��1+ ![]() ����
���� ![]() ����
����
������������P���������� ![]() ��
�� ![]() ����1��
����1�� ![]() ����
���� ![]() ����P�壨��1+
����P�壨��1+ ![]() ����
���� ![]() ����
����
����������1��Ҫ�����ʽ�ؼ�������B�����꣬�ɡ�ABCΪ����ֱ�������Σ���C=90�㣬BC=AC=5�������B����4����5������A��B����������ʽ���ɣ���2������ֵ����ɻ���Ϊ������ֵ���⣬����빹����E�������tΪ�Ա�����EF����Ϊ������ĺ�������t�Ĵ���ʽ��ʾEF��EF����ֱ�߶Σ��䳤�ȿ����϶˵���������¶˵������꣬�������������Ƕ��κ��������䷽�������ֵ����3����EFΪֱ�DZߵ�ֱ�������οɷ�Ϊ���ࣺ��EΪֱ�Ƕ��㣻��FΪֱ�Ƕ��㣻������E��F�ֱ���EF�Ĵ��� �������ߵĽ������P��.


 ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������续������ʪ�أ���������ˮ�����������ȹ���![]() ������ˮ�����豸��20̨����ʪ���ܱ���ˮ���д�����ÿ̨
������ˮ�����豸��20̨����ʪ���ܱ���ˮ���д�����ÿ̨![]() ����ˮ�����豸12��ÿ̨
����ˮ�����豸12��ÿ̨![]() ����ˮ�����豸10����֪2̨
����ˮ�����豸10����֪2̨![]() ����ˮ�����豸��1̨
����ˮ�����豸��1̨![]() ����ˮ�����豸ÿ�ܴ�����ˮ680�֣�3̨
����ˮ�����豸ÿ�ܴ�����ˮ680�֣�3̨![]() ����ˮ�����豸��2̨
����ˮ�����豸��2̨![]() ����ˮ�����豸ÿ�ܴ�����ˮ1120�֣�
����ˮ�����豸ÿ�ܴ�����ˮ1120�֣�
��1����ÿ̨![]() ��
��![]() ����ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
����ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2����Ԥ�㣬��ˮ�����������豸���ʽ���230��Ԫ��ÿ�ܴ�����ˮ����������4500�֣����оٳ����й�������ָ�����蹺���ʽ����ٵķ����������ʽ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������н�����ͼ��ʾ��ƽ��ֱ������ϵxOy.��ABC���������㶼�ڸ����,��A��������(4,4),������������:

(1)����ABC����ƽ��5����λ����,����ƽ�ƺ��A1B1C1,��д����A�Ķ�Ӧ��A1������;
(2)������A1B1C1����y��ԳƵġ�A2B2C2;
(3)����ABC�Ƶ�C��ʱ����ת90��,������ת��ġ�A3B3C.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ӣ����![]() ������־�����30���ֻ������˼�⣬��������н��ķ�֮һ���ֻ�Я����ϸ�������ﵽ�ɽ���������10��������һ��������ֻ�һ�����������˳��������������������ֻ��Ϸ��ֵ��к�ϸ���У���Ϊ�������к�ϸ���������ɫ�������������ϸ���ɵ���һϵ�и�Ⱦ�����ɫ�������Ϊ���Σ�ֱ��
������־�����30���ֻ������˼�⣬��������н��ķ�֮һ���ֻ�Я����ϸ�������ﵽ�ɽ���������10��������һ��������ֻ�һ�����������˳��������������������ֻ��Ϸ��ֵ��к�ϸ���У���Ϊ�������к�ϸ���������ɫ�������������ϸ���ɵ���һϵ�и�Ⱦ�����ɫ�������Ϊ���Σ�ֱ��![]() ���ң�0��0000008��������ÿ�ѧ��������ʾΪ�� ��
���ң�0��0000008��������ÿ�ѧ��������ʾΪ�� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AD��BC�ڵ�D��AEΪ��BAC��ƽ���ߣ��ҡ�B��36�㣬��C��66�㣮���DAE�Ķ�����
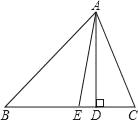
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ķ��������ѧС̽��ϵ�У��������������⣺
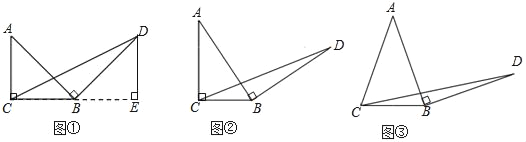
��1��̽��1����ͼ�٣��ڵ���ֱ��������ABC�У���ACB��90�㣬BC��3������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD������D��BC���ϵĸ�DE����DE��BC��������ϵ���� ������BCD�����Ϊ�� ����
��2��̽��2����ͼ�ڣ���һ���Rt��ABC�У���ACB��90�㣬BC��a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD�����ú�a��ʽ�ӱ�ʾ��BCD���������˵�����ɣ�
��3��̽��3����ͼ�ۣ��ڵ���������ABC�У�AB��AC��BC��a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD����̽���ú�a��ʽ�ӱ�ʾ��BCD�������Ҫ��̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
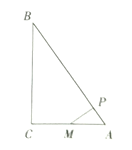
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AM=CM��MP��AB�ڵ�P.��֤��BP2=AP2+BC2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
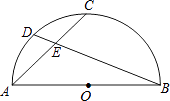
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������C�� ![]() ���е㣬��D��
���е㣬��D�� ![]() ���е㣬����AC��BD���ڵ�E����
���е㣬����AC��BD���ڵ�E���� ![]() =�� ��
=�� ��
A.![]()
B.![]()
C.1�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽����꼶ѧ�������������������˸�У������ѧ������������ϲ����������������������Ϊ���ࣺA����ϲ����ƹ������ˣ�B����ϲ����������ˣ�C����ϲ����������ˣ�D����ϲ���������ˣ����������������Ƴ�����������������ͳ��ͼ��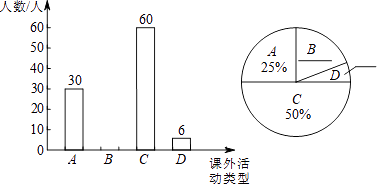
����ͳ��ͼ��Ϣ����������⣺
��1�������ѧ������Ϊ�ˣ�
��2����ȫ����ͳ��ͼ������ͳ��ͼ��
��3������У���꼶����600�ˣ���������꼶ѧ����ϲ����ƹ�����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com