
����Ŀ��Ϊ���������续������ʪ�أ���������ˮ�����������ȹ���![]() ������ˮ�����豸��20̨����ʪ���ܱ���ˮ���д�����ÿ̨
������ˮ�����豸��20̨����ʪ���ܱ���ˮ���д�����ÿ̨![]() ����ˮ�����豸12��ÿ̨
����ˮ�����豸12��ÿ̨![]() ����ˮ�����豸10����֪2̨
����ˮ�����豸10����֪2̨![]() ����ˮ�����豸��1̨
����ˮ�����豸��1̨![]() ����ˮ�����豸ÿ�ܴ�����ˮ680�֣�3̨
����ˮ�����豸ÿ�ܴ�����ˮ680�֣�3̨![]() ����ˮ�����豸��2̨
����ˮ�����豸��2̨![]() ����ˮ�����豸ÿ�ܴ�����ˮ1120�֣�
����ˮ�����豸ÿ�ܴ�����ˮ1120�֣�
��1����ÿ̨![]() ��
��![]() ����ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
����ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2����Ԥ�㣬��ˮ�����������豸���ʽ���230��Ԫ��ÿ�ܴ�����ˮ����������4500�֣����оٳ����й�������ָ�����蹺���ʽ����ٵķ����������ʽ�
���𰸡���1��![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣���2����һ�ַ�����������
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣���2����һ�ַ�����������![]() ����ˮ�����豸13̨������
����ˮ�����豸13̨������![]() ����ˮ�����豸7̨���ڶ��ַ�����������
����ˮ�����豸7̨���ڶ��ַ�����������![]() ����ˮ�����豸14̨������
����ˮ�����豸14̨������![]() ����ˮ�����豸6̨�������ַ�����������
����ˮ�����豸6̨�������ַ�����������![]() ����ˮ�����豸15̨������
����ˮ�����豸15̨������![]() ����ˮ�����豸5̨��Ӧ��ѡ���һ�ַ������ʽ�������226��Ԫ
����ˮ�����豸5̨��Ӧ��ѡ���һ�ַ������ʽ�������226��Ԫ
��������
��1����![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ![]() �֣�
�֣�![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ![]() �֣���������õ���Ԫһ�η����鼴����⣻
�֣���������õ���Ԫһ�η����鼴����⣻
��2���蹺��![]() ����ˮ�����豸
����ˮ�����豸![]() ̨������
̨������![]() ����ˮ�����豸
����ˮ�����豸![]() ̨����������õ�����ʽ�飬���ɵõ�3�ַ������ֱ�����������ķ��ü��ɱȽ���⣮
̨����������õ�����ʽ�飬���ɵõ�3�ַ������ֱ�����������ķ��ü��ɱȽ���⣮
�⣺��1����![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ![]() �֣�
�֣�![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ![]() �֣�
�֣�
![]()
���![]()
��![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�![]() ����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���蹺��![]() ����ˮ�����豸
����ˮ�����豸![]() ̨������
̨������![]() ����ˮ�����豸
����ˮ�����豸![]() ̨��
̨��
��![]()
��ã�![]() ��
��
��![]() ��������
��������![]() ��14��15
��14��15
��һ�ַ�����������![]() ����ˮ�����豸13̨������
����ˮ�����豸13̨������![]() ����ˮ�����豸7̨��
����ˮ�����豸7̨��
�ڶ��ַ�����������![]() ����ˮ�����豸14̨������
����ˮ�����豸14̨������![]() ����ˮ�����豸6̨��
����ˮ�����豸6̨��
�����ַ�����������![]() ����ˮ�����豸15̨������
����ˮ�����豸15̨������![]() ����ˮ�����豸5̨��
����ˮ�����豸5̨��
����һ�ַ��������ʽ�![]() ��Ԫ��
��Ԫ��
�ڶ��ַ��������ʽ�![]() ��Ԫ��
��Ԫ��
�����ַ��������ʽ�![]() ��Ԫ��
��Ԫ��
�ӽ�Լ�ʽ�ĽǶȿ��ǣ�Ӧ��ѡ���һ�ַ�����������![]() ����ˮ�����豸13̨������
����ˮ�����豸13̨������![]() ����ˮ�����豸7̨��
����ˮ�����豸7̨��
��ѡ���һ�ַ��������ʽ����٣�������226��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ��ֱ�DZ߳�Ϊ1��һ������ֱ��������ֽƬ����ͼ1���������ĶԳ����۵�1�κ�õ�һ������ֱ�������Σ���ͼ2�����ٽ�ͼ2�ĵ���ֱ�������������ĶԳ����۵���õ�һ������ֱ�������Σ���ͼ3������ͼ3�еĵ���ֱ�������ε�һ������Ϊ��ͬ�ϲ�������С��������ͼ1�ĵ���ֱ���������۵�n�κ����õ��ĵ���ֱ�������Σ���ͼn+1����һ������Ϊ �� 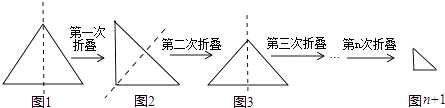
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����գ���֪����ͼ��![]() ��
��![]() ��
��![]() ������ͬһֱ���ϣ�
������ͬһֱ���ϣ�![]() ��
��![]() ��
��![]() ������ͬһֱ���ϣ�
������ͬһֱ���ϣ�![]() ��
��![]() ����֤��
����֤��![]() ��
��
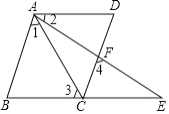
֤������![]()
��________���ڴ�����ȣ���ֱ��ƽ�У�
��![]() ________����ֱ��ƽ�У��ڴ�����ȣ�
________����ֱ��ƽ�У��ڴ�����ȣ�
��![]()
��![]() ��________________��
��________________��
��![]()
��![]() ����________________��
����________________��
��![]() ________
________
��![]()
��![]() ��ͬλ����ȣ���ֱ��ƽ�У���
��ͬλ����ȣ���ֱ��ƽ�У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��![]()
��2��20142-2018 �� 2010
��3��(x+2y-3)(x-2y-3)
��4��![]()
��5���Ȼ�����ֵ�� ![]() ������
������![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
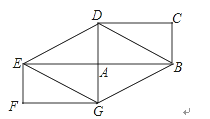
����Ŀ����ͼ������ABCD�;���AEFG���ڵ�A���ĶԳƣ�
��1���ı���BDEG����������˵�����ɣ�
��2��������ABCD���Ϊ8�����ı���BDEG�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ���![]() �У�
��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ�㣨����
��һ�㣨����![]() �غϣ�����
�غϣ�����![]() Ϊһ����
Ϊһ����![]() ���Ҳ�������
���Ҳ�������![]() ��ʹ
��ʹ![]() ��
��![]() ������
������![]() ��
��
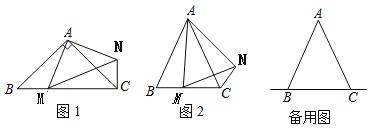
��1����ͼ1������![]() ���߶�
���߶�![]() ��ʱ�����
��ʱ�����![]() ����
����![]() _______�㣮
_______�㣮
��2����![]() ��
��
����ͼ2������![]() ���߶�
���߶�![]() ���ƶ�ʱ��
���ƶ�ʱ��![]() ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�
�ڵ���![]() ��ֱ��
��ֱ��![]() ���ƶ�ʱ��
���ƶ�ʱ��![]() ֮����������������ϵ������ֱ��д����Ľ��ۣ�
֮����������������ϵ������ֱ��д����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD���ڵ�O��AEƽ����BAD��BC�ڵ�E������ADC=60�㣬AB=![]() BC������OE�����н��ۣ��١�CAD=30�㣻��SABCD=ABAC����OB=AB����OE=
BC������OE�����н��ۣ��١�CAD=30�㣻��SABCD=ABAC����OB=AB����OE=![]() BC�������ĸ����У�������
BC�������ĸ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬��D��E�ֱ��DZ�BC��AB�ϵ��е㣬����DE���ӳ�����F��ʹEF=2DE������CE��AF��
��1��֤����AF=CE��
��2������B=30��ʱ�����ж��ı���ACEF����״��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABCΪ����ֱ�������Σ���ACB=90�㣬������y=��x2+bx+c����A��B���㣬���е�A��C������ֱ�Ϊ��1��0��������4��0���������ߵĶ���Ϊ��D��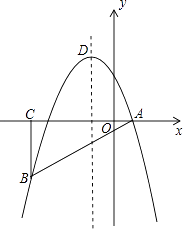
��1���������ߵĽ���ʽ��
��2����E��ֱ��������ABCб��AB�ϵ�һ�����㣨����A��B�غϣ�������E��x��Ĵ��ߣ����������ڵ�F�����߶�FE�ij������ʱ�����E�����ꣻ
��3���ڣ�2���������£����������Ƿ����һ��P��ʹ��PEF����EFΪֱ�DZߵ�ֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com