
【题目】如图,以正六边形![]() 的对角线
的对角线![]() 为边,向右作等边三角形
为边,向右作等边三角形![]() ,若四边形
,若四边形![]() 的面积为4,则五边形
的面积为4,则五边形![]() 的面积为( )
的面积为( )

A.6B.8C.10D.12
【答案】C
【解析】
连接GC并延长交BD于点H,连接AE,根据正六边形和等边三角形的性质可得,△BCG≌△DCG,△GBC≌△DBC,所以得S△BCG=S△DCG=S△BCD=2,S△AEF=2,进而可得五边形ABDEF的面积.
解:如图,连接GC并延长交BD于点H,连接AE,
∵ABCDEF正六边形,
∴AB=BC=CD=DE=EF=AF,
∠F=∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=120°,
∵△BDG是等边三角形,
∴BG=DG=BD
又CG=CG,
∴△BCG≌△DCG(SSS),
∵∠GBC=∠DBC=30°,
∴△GBC≌△DBC(SAS),
∴S△BCG=S△DCG=S△BCD=2,
∴S△AEF=2,
设CH=x,则BC=CG=2x,BH=![]() ,
,
∴BD=![]() ,
,
∴![]() CGBH=2,
CGBH=2,
即![]() ×2x×
×2x×![]() =2,
=2,
∴![]() ,
,
∴S四边形ABDE=ABBD=2x2![]() =4
=4![]() =8,
=8,
∴五边形ABDEF的面积为:2+8=10.
故选:C.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,过点
上的点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() .
.
(1)填空:点![]() _____________(填“在”或“不在”)
_____________(填“在”或“不在”)![]() 上;当
上;当![]() 时,
时,![]() 的值是_____________;
的值是_____________;
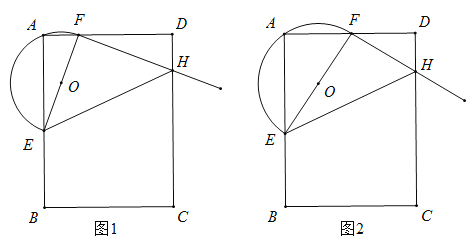
(2)如图1,在![]() 中,当
中,当![]() 时,求证:
时,求证:![]() ;
;
(3)如图2,当![]() 的顶点
的顶点![]() 是边
是边![]() 的中点时,请直接写出
的中点时,请直接写出![]() 三条线段的数量关系.
三条线段的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
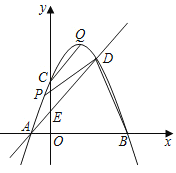
(1)连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)连接![]() ,
,![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出点
为等腰直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在三角形纸片ABC中,∠BAC=78°,AC=10.数学实践课上,小敏用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2所示),并通过上网查到以下几个数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.7.请你帮助她解决下列问题:

(1)∠ABC= °;
(2)求正五边形GHMNC的边GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABC是等腰直角三角形,∠B=90°,点B的坐标为(1,2).反比例函数![]() 的图象经过点C,一次函数y=ax+b的图象经A,C两点.
的图象经过点C,一次函数y=ax+b的图象经A,C两点.
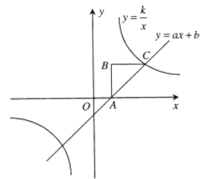
(1)求反比例函数和一次函数的关系式;
(2)直接写出不等式组0<ax+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)若![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,二次函数
时,二次函数![]() 有最大值
有最大值![]() ,求
,求![]() 的值;
的值;
(3)直线![]() 与直线
与直线![]() 、直线
、直线![]() 分别相交于
分别相交于![]() 、
、![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() (包含
(包含![]() 、
、![]() 两点)有两个公共点,求
两点)有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=![]() (k<0)的图象上.则y1、y2、y3的大小关系是( )
(k<0)的图象上.则y1、y2、y3的大小关系是( )
A.y1>y2>y3B.y3>y2>y1C.y2>y3>y1D.y1>y3>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在九年级复学复课以后,随机抽取九年级(3)班5名学生的一次晨检体温测量值(单位:℃)如下: 36.9,36.8,36.8,36.5,37.关于这组数据的说法错误的是( )
A.众数是36.8B.平均数是36.8C.中位数是36.8D.方差是0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经营一款新电动玩具,进货单价是30元。在1个月的试销阶段,售价是40元,销售量是400件.根据市场调查,销售单价若每再涨1元,1个月就会少售出10件.
(1)若商店在1个月获得了6000元销售利润,求这款玩具销售单价是定为多少元的,并考虑了顾客更容易接受.
(2)若玩具生产厂家规定销售单价不低于43元,且商店每月要完成不少于350件的销售任务,求商店销售这款玩具1个月能获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com