
��ͼ����֪l1��l2����O��l1��l2�����У���O�İ뾶Ϊ2cm������ABCD�ı�AD��AB�ֱ���l1��l2�غϣ�AB��4 cm��AD��4cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ3cm/s������ABCD���ƶ��ٶ�Ϊ4cm/s�����ƶ�ʱ��Ϊt(s)��
cm��AD��4cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ3cm/s������ABCD���ƶ��ٶ�Ϊ4cm/s�����ƶ�ʱ��Ϊt(s)��
��1����ͼ��������OA��AC������OAC�Ķ���Ϊ �㣻
��2����ͼ��������ͼ���ƶ�һ��ʱ�����O������O1��λ�ã�����ABCD����A1B1C1D1��λ�ã���ʱ��O1��A1��C1ǡ����ͬһֱ���ϣ���Բ��O�ƶ��ľ���(��OO1�ij�����
��3�����ƶ������У�Բ��O�����ζԽ���AC����ֱ�ߵľ����ڲ��ϱ仯����þ���Ϊd(cm)����d<2ʱ����t��ȡֵ��Χ�������ʱ�������ñ���ͼ�������ʾ��ͼ��

��1��105����2��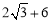 ����3��
����3��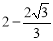 ��t��
��t��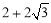 .
.
��������
�����������1����O��l1��l2�����У�����Բ�ĺ������е㣬��������.OA��Ϊ�����εĶԽ��ߣ��õ���OAD=450������Rt��ADC�У���������Ǻ�������DAC=600���Ӷ������OAC�Ķ���1050.
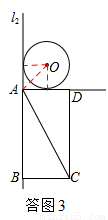
��2������O1���е�E����O1E=2��O1E��l1��������O1EA1�ס�D1C1E1,��A1E=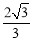 ������2+O1O+A1E=AA1������t���������Բ���ƶ��ľ���3t=
������2+O1O+A1E=AA1������t���������Բ���ƶ��ľ���3t=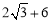 .
.
��3��Բ��O���Խ���AC�ľ���d��2����d��r.˵����O��AC�ཻ�����Գ��������ٽ���tֵ������O��AC�������˶��д����������е�λ��.�ֱ�����������ʱt��ֵ�����ɵó�d��rʱ��t��ȡֵ
�����������������
��1��1050.
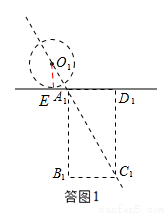
��2��O1��A1��C1ǡ����ͬһֱ����ʱ������O��AC���е�ΪE������O1E�����ͼ1��
�ɵ�O1E=2��O1E��l1��
��Rt��A1D1C1����A1D1=4��D1C1= ��
��
��tan��C1A1D1=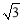 �����C1A1D1=600��
�����C1A1D1=600��
��Rt��A1O1E��, ��O1A1E=��C1A1D1=600����A1E=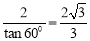 ,
,
��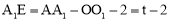 ����
����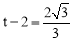 ����
����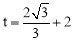 .
.
��OO1=3t=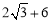 .
.
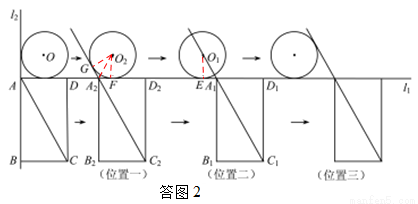
��3�����ͼ2��
����ֱ��AC����O��һ������ʱ�����ƶ�ʱ��Ϊt1.��λ��һ����ʱ��O�ƶ�����O2��λ�ã�����ABCD�ƶ���A2B2C2D2��λ��.
����O2��ֱ��l1��A2C2�ֱ������ڵ�F��G, ����O2 F��O2 G��O2 A2��
��O2 F��l1��O2 G��A2C2.
���ɣ�2���ɵ���C2A2D2=600�ڣ����GA2F=1200�����O2A2F=600.
��Rt��O2A2F��O2F=2����A2F=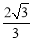 .
.
��OO2=3t1�� 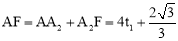 ����
����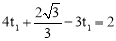 �����
�����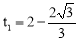 .
.
������O1��A1��C1ǡ����ͬһֱ����ʱΪλ�ö������ƶ�ʱ��Ϊt2.����2���ɵ�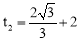 .
.
����ֱ��AC����O�ڶ�������ʱ�����ƶ�ʱ��Ϊt3����λ��3��������֪����λ��һ��λ�ö�����ʱ����λ�ö���λ��������ʱ�����.
��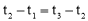 ����
����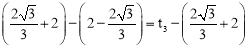 �����
�����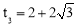 .
.
������������d<2ʱ��t��ȡֵ��ΧΪ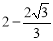 ��t��
��t��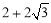 .
.
���㣺1.˫�涯ƽ�����⣻2.ֱ����Բ��λ�ù�ϵ��3.������Ǻ������壻4������ǵ����Ǻ���ֵ�� 5.����˼���Ӧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ������ϲ�������ѧ�������棩 ���ͣ�ѡ����
��֪����������y= ��ͼ����ͼ������κ���y=2kx2��4x+k2��ͼ�����Ϊ��������
��ͼ����ͼ������κ���y=2kx2��4x+k2��ͼ�����Ϊ��������

A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������Ƹ۾�����ѧ�������棩 ���ͣ������
һ��������ε�һ����ǵ���30�㣬�����������εı���Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������Ƹ۾�����ѧ�������棩 ���ͣ�ѡ����
��˿��֮·�����ô���ʵ��ƽ̨�����й�������������������Ͷ��ʹ�ã������װж������410 000���䣬���С�410 000���ÿ�ѧ��������ʾΪ
A��0��41��106 B�� 4.1��105 C��41��104 D��4.1��104
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ������
��ͼ����Rt��ABC�У���ACB��90�㣬��D��F�ֱ���AB��AC�ϣ�CF��CB������CD�����߶�CD�Ƶ�C��˳ʱ�뷽����ת90����CE������EF��
��1����֤����BCD����FCE��
��2����EF��CD������BDC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������ݾ�����ѧ�������棩 ���ͣ������
ij������һ�γ�120m�ĺӵ�����������ͨ�������̶�����4�쵥���������һ���ֺӵ�����ͨ���������µ��������ҹ��̶ӵ��������Ҫ9�죻�����̶��ȵ�������8�죬�����µ��������ҹ��̶ӵ��������Ҫ3�죬����̶�ƽ��ÿ����ͨ�ӵ�xm���ҹ��̶�ƽ��ÿ����ͨ�ӵ�ym����x��y����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����ջ���������ѧ�������棩 ���ͣ������
��ͼ����A��1��6���͵�M��m��n�����ڷ���������y= ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��1��k��ֵΪ�� ����
��2����m=3����ֱ��AM�Ľ���ʽ��
��3����m��1ʱ������M��MP��x�ᣬ����ΪP������A��AB��y�ᣬ����ΪB�����ж�ֱ��BP��ֱ��AM��λ�ù�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ���������������ѧ�������棩 ���ͣ������
��ͼ��?ABCD�У�AE��BD��E����EAC=30�㣬AE=3����AC�ij����� ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com