
如图,点A(1,6)和点M(m,n)都在反比例函数y= (x>0)的图象上,
(x>0)的图象上,
(1)k的值为 ;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.

(1)6
(2)直线AM解析式为y=﹣2x+8;
(3)直线BP与直线AM的位置关系为平行,理由见解析
【解析】
试题分析:(1)将A坐标代入反比例解析式求出k的值即可;
(2)由k的值可得反比例解析式,将x=3代入反比例解析式求出y的值,从而确定M坐标,由待定系数法即可求出直线AM解析式;
(3)由MP垂直于x轴,AB垂直于y轴,得到M与P横坐标相同,A与B纵坐标相同,表示出B与P坐标,分别求出直线AM与直线BP斜率,由两直线斜率相等,得到两直线平行.
试题解析:(1)将A(1,6)代入反比例解析式得:k=6;
(2)将x=3代入反比例解析式y=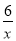 得:y=2,即M(3,2),
得:y=2,即M(3,2),
设直线AM解析式为y=ax+b,
把A与M代入得: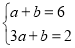 ,
,
解得:a=﹣2,b=8,
∴直线AM解析式为y=﹣2x+8;
(3)直线BP与直线AM的位置关系为平行,理由为:
当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,
∵A(1,6),M(m,n),且mn=6,即n= ,
,
∴B(0,6),P(m,0),
∴k直线AM= =
=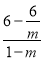 =
=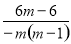 =
=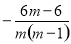 =﹣
=﹣ ,k直线BP=
,k直线BP=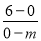 =﹣
=﹣ ,即k直线AM=k直线BP,
,即k直线AM=k直线BP,
则BP∥AM.
考点:1、待定系数法;2、反比例函数;3、一次函数;4、直线的斜率


科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
(1)如图①,连接OA,AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:选择题
若式子 可在实数范围内有意义,则x的取值范围是( )
可在实数范围内有意义,则x的取值范围是( )
A.x≤-4 B.x≥-4 C.x≤4 D.x≥4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:解答题
班级准备召开主题班会,现从由3名男生和2名女生所组成的班委中,随机选取两人担任主持人,求两名主持人恰为一男一女的概率.(请用“画树状图”或“列表”等方法写出过程)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:填空题
在平面直角坐标系中,将点A(4,2)绕原点逆时针方向旋转90°后,其对应点A′的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com