
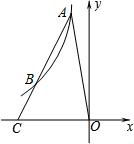
 如图,点A、B在双曲线y=$\frac{k}{x}$上,AB的延长线交x轴于C,连OA.若AB=2BC,S△OAC=12,则k=-6.
如图,点A、B在双曲线y=$\frac{k}{x}$上,AB的延长线交x轴于C,连OA.若AB=2BC,S△OAC=12,则k=-6. 分析 作AD⊥x轴于D,BE⊥x轴于E,如图,先证明△CEB∽△CDA得到$\frac{CB}{AB}$=$\frac{CE}{DE}$=$\frac{1}{2}$,$\frac{BE}{AD}$=$\frac{CB}{CA}$=$\frac{1}{3}$,根据反比例函数图象上点的坐标特征可设B($\frac{k}{t}$,t),则A($\frac{k}{3t}$,3t),则DE=$\frac{-2k}{3t}$,CE=$\frac{1}{2}$DE=-$\frac{k}{3t}$,然后根据三角形面积公式得到$\frac{1}{2}$•3t•(-$\frac{4k}{3t}$)=12,再解关于k的方程即可.
解答 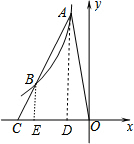 解:作AD⊥x轴于D,BE⊥x轴于E,如图,
解:作AD⊥x轴于D,BE⊥x轴于E,如图,
∵BE∥AD,
∴△CEB∽△CDA,
∴$\frac{CB}{AB}$=$\frac{CE}{DE}$=$\frac{1}{2}$,$\frac{BE}{AD}$=$\frac{CB}{CA}$=$\frac{1}{3}$,
设B($\frac{k}{t}$,t),则A($\frac{k}{3t}$,3t),
∴DE=$\frac{k}{3t}$-$\frac{k}{t}$=$\frac{-2k}{3t}$,
∴CE=$\frac{1}{2}$DE=-$\frac{k}{3t}$,
∵S△OAC=12,
∴$\frac{1}{2}$•3t•(-$\frac{4k}{3t}$)=12,
∴k=-6.
故答案为-6.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<-1 | B. | a<1 | C. | a>-1 | D. | a>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
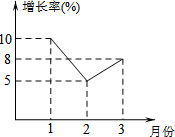 武汉市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图.下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长.其中正确的结论是( )
武汉市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图.下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长.其中正确的结论是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个表面涂满色的正方体.
一个表面涂满色的正方体.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com