
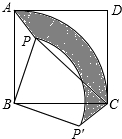
 已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.分析 (1)根据旋转的性质得到S△ABP=S△CBP′,根据扇形的面积公式计算即可;
(2)连接PP′,根据勾股定理计算即可.
解答 解:(1)由旋转的性质可知,S△ABP=S△CBP′,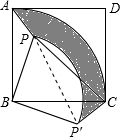
∴△PAB旋转过程中边PA扫过区域面积=$\frac{90π×{m}^{2}}{360}$-$\frac{90π×{n}^{2}}{360}$=$\frac{π}{4}$(m2-n2);
(2)连接PP′,
由旋转的性质可知,∠BP′C=∠APB=135°,∠PBP′=90°,BP′=BP=2$\sqrt{2}$,P′C=PA=$\sqrt{2}$,
∴PP′=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,∠PP′C=90°,
∴PC=$\sqrt{{4}^{2}+(\sqrt{2})^{2}}$=3$\sqrt{2}$.
点评 本题考查的是旋转的性质、扇形面积的计算,掌握旋转变换的性质、扇形的面积公式是解题的关键.


科目:初中数学 来源: 题型:解答题
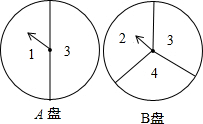 甲乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图,游戏规则;甲乙两同学分别转动AB两个转盘,当转盘停止后,指针所在区或的数字之和为偶数时甲胜;数字之和为奇数时乙胜,若指针恰好在分割线上,则需要重新转动转盘.
甲乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图,游戏规则;甲乙两同学分别转动AB两个转盘,当转盘停止后,指针所在区或的数字之和为偶数时甲胜;数字之和为奇数时乙胜,若指针恰好在分割线上,则需要重新转动转盘.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
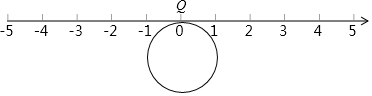
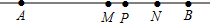 已知:点B在直线AP上,点M、N分别是线段AB、BP的中点,如图,点B在线段AP的延长线上,AM-PN=3.5,点C为直线AB上一点,CA+CP=13,求CP的长度.
已知:点B在直线AP上,点M、N分别是线段AB、BP的中点,如图,点B在线段AP的延长线上,AM-PN=3.5,点C为直线AB上一点,CA+CP=13,求CP的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com