
【题目】如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y= ![]() 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )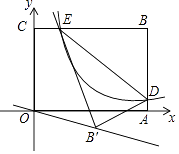
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】∵矩形OABC,
∴CB∥x轴,AB∥y轴,
∵点B坐标为(6,4),
∴D的横坐标为6,E的纵坐标为4,
∵D,E在反比例函数y= ![]() 的图象上,
的图象上,
∴D(6,1),E( ![]() ,4),
,4),
∴BE=6﹣ ![]() =
= ![]() ,BD=4﹣1=3,
,BD=4﹣1=3,
∴ED= ![]() =
= ![]() ,
,
连接BB′,交ED于F,过B′作B′G⊥BC于G, 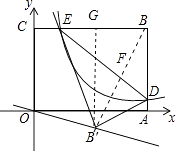
∵B,B′关于ED对称,
∴BF=B′F,BB′⊥ED,
∴BFED=BEBD,
即 ![]() BF=3×
BF=3× ![]() ,
,
∴BF= ![]() ,
,
∴BB′= ![]() ,
,
设EG=x,则BG= ![]() ﹣x,
﹣x,
∵BB′2﹣BG2=B′G2=EB′2﹣GE2,
∴( ![]() )2﹣(
)2﹣( ![]() ﹣x)2=(
﹣x)2=( ![]() )2﹣x2,
)2﹣x2,
∴x= ![]() ,
,
∴EG= ![]() ,
,
∴CG= ![]() ,
,
∴B′G= ![]() ,
,
∴B′( ![]() ,﹣
,﹣ ![]() ),
),
∴k=﹣ ![]() .
.
所以答案是:B.
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.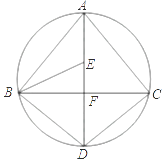
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.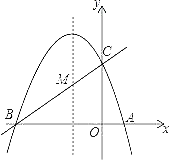
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织教师为地震救灾捐款,分6个工会小组进行统计,其中第6工会小组尚未统计在内,如图:
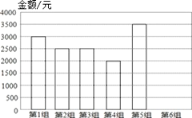
(1)求前5个工会小组捐款金额的众数、中位数和平均数;
(2)若全部6个小组的捐款平均数为2750元,求第6小组的捐款金额,并补全统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= ![]() (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE= ![]() ,则BN的长为 .
,则BN的长为 . 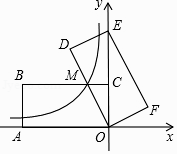
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )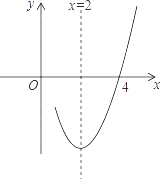
A.①②③
B.③④⑤
C.①②④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com