
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )

A.4B.3C.2D.1
【答案】B
【解析】
①利用HL证明可得;
②设AG=x,在△GBE中,利用勾股定理可得到关于x的方程,解得x的值,从而得出GF、GB的值;
③△GDF是直角三角形,直接按照面积公式求解即可;
④先求解出Rt△GBE的面积,△EBF的面积=△GBE的面积×![]() .
.
①∵△EDF是△EDC翻折得到,∴△EDF≌△EDC
∴DF=CD=AD=12,∠EFD=∠ECD=90°=∠GAD
∵GD=GD
∴△FGD≌△AGD,①正确
②设AG=x,则GF=x,GB=12-x
∵BE=EC,∴BE=EC=FE=6
∴在Rt△GBE中,![]() ,即:
,即:![]()
解得:x=4,∴AG=GF=4,BG=8,②正确
③![]() ,③错误
,③错误
④![]()
∴![]() ,④正确
,④正确
故选:B


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y= ![]() 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )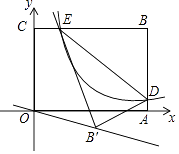
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴围成的
轴围成的![]() 的面积为
的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 坐标并判断
坐标并判断![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的面积为
的面积为![]() ,求
,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场调查表明:某种一周内水果的销售率y(销售率= ![]() )与价格倍数x(价格倍数=
)与价格倍数x(价格倍数= ![]() )的关系满足函数关系y=﹣
)的关系满足函数关系y=﹣ ![]() x+
x+ ![]() (1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120%
B.80%
C.60%
D.40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2018年举行迎新春首届灯展,承办方计划在现场安装小彩灯和大彩灯,已知:安装5个小彩灯和4个大彩灯共需155元;安装7个小彩灯和6个大彩灯共需225元.
(1)安装1个小彩灯和1个大彩灯各需多少元.
(2)若承办方安装小彩灯和大彩灯的数量共300个,费用不超过5000元,则最多安装大彩灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.
其中正确的结论的有( )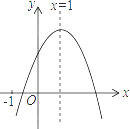
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于代数式 ![]() 的值的情况,小明作了如下探究的结论,其中错误的是( )
的值的情况,小明作了如下探究的结论,其中错误的是( )
A.只有当 ![]() 时,
时, ![]() 的值为2
的值为2
B.![]() 取大于2的实数时,
取大于2的实数时, ![]() 的值随
的值随 ![]() 的增大而增大,没有最大值
的增大而增大,没有最大值
C.![]() 的值随
的值随 ![]() 的变化而变化,但是有最小值
的变化而变化,但是有最小值
D.可以找到一个实数 ![]() ,使
,使 ![]() 的值为0
的值为0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com